题目内容
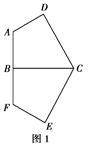
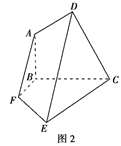
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 在
在![]() 上,且
上,且![]() ,又
,又![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)设OA=1,则PO=OB=2,DA=1,由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,可得DA⊥AO.利用勾股定理的逆定理可得:PD⊥DO.由OC=OB=2,∠ABC=45°,可得CO⊥AB,又PO⊥平面ABC,可得PO⊥OC,得到CO⊥平面PAB.得到CO⊥PD.即可证明.
(Ⅱ)如图建立空间直角坐标系,点A为坐标原点,设AB=1,利用线面垂直的性质、向量垂直与数量积的关系得出两个平面的法向量,求出其夹角即可.
详解:(Ⅰ)证明:设OA=1,则PO=OB=2,DA=1,
由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,
∴DA⊥AO.从而![]() ,
,
在△PDO中,∵PO=2,
∴△PDO为直角三角形,故PD⊥DO.
又∵OC=OB=2,∠ABC=45°,
∴CO⊥AB,又PO⊥平面ABC,
∴PO⊥OC,
又PO,AB平面PAB,PO∩AB=O,
∴CO⊥平面PAB.
故CO⊥PD.
∵CO∩DO=O,
∴PD⊥平面COD.
(Ⅱ)解:以OC,OB,OP所在射线分别为x,y,z轴,建立直角坐标系如图.
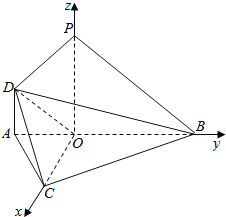
则由(Ⅰ)知,C(2,0,0),B(0,2,0),P(0,0,2),D(0,﹣1,1),
∴![]() ,
,
由(Ⅰ)知PD⊥平面COD,∴![]() 是平面DCO的一个法向量,
是平面DCO的一个法向量,
设平面BDC的法向量为![]() ,∴
,∴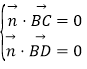 ,∴
,∴![]() ,
,
令y=1,则x=1,z=3,∴![]() ,
,
∴ ,
,
由图可知:二面角B﹣DC﹣O为锐角,二面角B﹣DC﹣O的余弦值为![]() .
.

练习册系列答案
相关题目