题目内容
【题目】已知函数![]() ,若
,若![]() 是函数
是函数![]() 的唯一极值点,则实数
的唯一极值点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:由f(x)的导函数形式可以看出ex﹣kx=0在(0,+∞)无变号零点,
令g(x)=ex﹣kx,g′(x)=ex﹣k,需要对k进行分类讨论来确定导函数为0时的根.
详解:∵函数![]() 的定义域是(0,+∞),
的定义域是(0,+∞),
∴f′(x)=![]() .
.
x=1是函数f(x)的唯一一个极值点
∴x=1是导函数f′(x)=0的唯一根.
∴ex﹣kx=0在(0,+∞)无变号零点,
令g(x)=ex﹣kx
g′(x)=ex﹣k
①k≤0时,g′(x)>0恒成立.g(x)在(0,+∞)时单调递增的
g(x)的最小值为g(0)=1,g(x)=0无解
②k>0时,g′(x)=0有解为:x=lnk
0<x<lnk时,g′(x)<0,g(x)单调递减
lnk<x时,g′(x)>0,g(x)单调递增
∴g(x)的最小值为g(lnk)=k﹣klnk
∴k﹣klnk>0
∴k<e,
由y=ex和y=ex图象,它们切于(1,e),
综上所述,k≤e.
故答案为:A.

 阅读快车系列答案
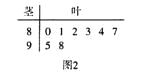
阅读快车系列答案【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
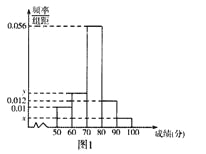
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
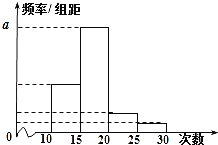
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
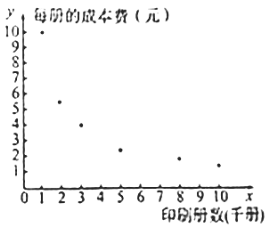
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: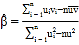 ,
,![]() .
.