题目内容
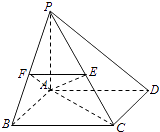
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知AB=2，AD=2 
，PA=2，求： 
（1）三角形PCD的面积；
（2）异面直线BC与AE所成的角的大小．
【答案】
（1）解：∵PA⊥底面ABCD，CD底面ABCD，
∴CD⊥PA．
∵矩形ABCD中，CD⊥AD，而PA、AD是平面PAD的交线．
∴CD⊥平面PDA，
∵PD平面PDA，∴CD⊥PD，三角形PCD是以D为直角顶点的直角三角形．
∵Rt△PAD中，AD=2 
，PA=2，
∴PD= 
=2 
．
∴三角形PCD的面积S= 
×PD×DC=2 ．
（2）解：[解法一]
如图所示，建立空间直角坐标系，可得B（2，0，0），C（2，2 ，0），E（1， ，1）．
∴ 
=（1， ，1）， 
=（0，2 ，0），
设 与 夹角为θ，则cosθ=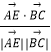 
= 
= 
，
∴θ= 
，由此可得异面直线BC与AE所成的角的大小为 ．
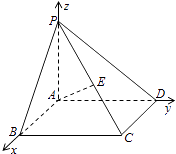
[解法二]
取PB的中点F，连接AF、EF、AC，
∵△PBC中，E、F分别是PC、PB的中点，
∴EF∥BC，∠AEF或其补角就是异面直线BC与AE所成的角．
∵Rt△PAC中，PC= 
=4．
∴AE= PC=2，
∵在△AEF中，EF= BC= ，AF= PB= 
∴AF2+EF2=AE2，△AEF是以F为直角顶点的等腰直角三角形，
∴∠AEF= ，可得异面直线BC与AE所成的角的大小为 ．
【解析】（1）可以利用线面垂直的判定与性质，证明出三角形PCD是以D为直角顶点的直角三角形，然后在Rt△PAD中，利用勾股定理得到PD=2 ，最后得到三角形PCD的面积S；（2）[解法一]建立如图空间直角坐标系，可得B、C、E各点的坐标，从而 =（1， ，1）， =（0，2 ，0），利用空间向量数量积的公式，得到 与 夹角θ满足：cosθ= ，由此可得异面直线BC与AE所成的角的大小为 ；[解法二]取PB的中点F，连接AF、EF，△PBC中，利用中位线定理，得到EF∥BC，从而∠AEF或其补角就是异面直线BC与AE所成的角，然后可以通过计算证明出：△AEF是以F为直角顶点的等腰直角三角形，所以∠AEF= ，可得异面直线BC与AE所成的角的大小为 ．
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的性质的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；垂直于同一个平面的两条直线平行才能正确解答此题．
