题目内容
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.
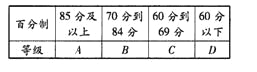
规定:![]() 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计.按照
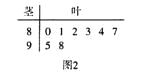
名学生的原始成绩作为样本进行统计.按照![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
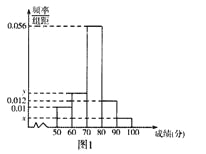
(I)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;
(II)在选取的样本中,从![]() 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是![]() 等级的概率.
等级的概率.
【答案】(I)![]() ,
,![]() ;(II)
;(II)![]() .
.
【解析】
试题(I)根据频率直方图的相关概率易求![]() ,依据样本估计总体的思想可得该校高一年级学生成绩是合格等级的概率;(II)记“至少有一名学生是
,依据样本估计总体的思想可得该校高一年级学生成绩是合格等级的概率;(II)记“至少有一名学生是![]() 等级”事件为
等级”事件为![]() ,求事件
,求事件![]() 对立事件
对立事件![]() 的的概率,可得
的的概率,可得![]() .
.
试题解析:(I)由题意可知,样本容量![]()
![]()
因为成绩是合格等级人数为:![]() 人,抽取的50人中成绩是合格等级的频率为
人,抽取的50人中成绩是合格等级的频率为![]() ,依据样本估计总体的思想,所以,该校高一年级学生成绩是合格等级的概率为
,依据样本估计总体的思想,所以,该校高一年级学生成绩是合格等级的概率为![]()
(II)由茎叶图知,![]() 等级的学生共有3人,
等级的学生共有3人,![]() 等级学生共有
等级学生共有![]() 人,记
人,记![]() 等级的学生为
等级的学生为![]() ,
,
![]() 等级学生为
等级学生为![]() ,则从8名学生中随机抽取2名学生的所有情况为:
,则从8名学生中随机抽取2名学生的所有情况为:![]()
![]()
![]() 共28个基本事件
共28个基本事件
记“至少有一名学生是![]() 等级”事件为
等级”事件为![]() ,则事件
,则事件![]() 的可能结果为
的可能结果为![]()
![]()
![]() 共10种
共10种
因此![]()

【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |