题目内容
9.定义在R上的函数f(x)满足f(x+2)=-f(x),当-2≤x≤-1时,f(x)=-(x+1)2,当-1<x<2时,f(x)=x,则f(1)+f(2)+…+f(2015)=( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由f(x+2)=-f(x)求出函数的周期,求出f(1)+f(2)+f(3)+f(4)的值.然后求解表达式的值.
解答 解:∵f(x+2)=-f(x),∴f(x+4)=f(x),
∴T=4,
∵当-2≤x≤-1时,f(x)=-(x+1)2,当-1<x<2时,f(x)=x,
∴f(1)=1,
f(2)=f(-2)=-1,
f(3)=f(-1)=0,
f(4)=f(0)=0,
∴f(1)+f(2)+f(3)+f(4)=0;
f(1)+f(2)+f(3)+…+f(2015)=503×0+f(1)+f(2)+f(3)=0.
故选:A.
点评 本题考查函数的周期性,抽象函数的应用,根据周期性求代数式的值,属于一道基础题.

练习册系列答案
相关题目
4.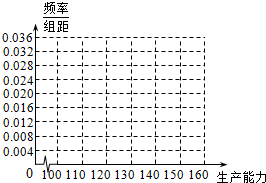 某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1:
表2:
先确定x、y,再完成频率分布直方图,并估计该工厂工人的生产能力的平均数.
 某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1:
| 生产能 力分组 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能 力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 36 | 18 |
19.函数y=${log_{\frac{1}{2}}}|{x+2}|$的增区间为( )
| A. | (-∞,+∞) | B. | (-∞,-2) | C. | (-2,+∞) | D. | (-∞,-2)∪(-2,+∞) |