题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}-{x^3}+{x^2},x<1\\ alnx,x≥1\end{array}$(1)求f(x)在区间[-1,1)上的最大值;
(2)对任意给定的正实数a,曲线y=f(x)上是否存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?说明理由.
分析 (1)当-1≤x<1时,求导函数,可得f(x)在区间[-1,1)上的最大值;
(2)假设曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.设P、Q的坐标,由此入手能得到对任意给定的正实数a,曲线y=f(x)上存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
解答 解:(1)∵$f(x)=\left\{\begin{array}{l}-{x^3}+{x^2},x<1\\ alnx,x≥1\end{array}\right.$
当-1≤x<1时,$f'(x)=-3{x^2}+2x=-3x(x-\frac{2}{3})$,…(1分)
令f'(x)=0得x=0或$x=\frac{2}{3}$,当x变化时,f'(x),f(x)的变化情况如下表:
| (-1,0) | 0 | $(0,\frac{2}{3})$ | $\frac{2}{3}$ | $(\frac{2}{3},1)$ | |
| - | 0 | + | 0 | - | |
| 递减 | 极小值 | 递增 | 极大值 | 递减 |
又f(-1)=2,$f(\frac{2}{3})=\frac{4}{27}$,f(0)=0
∴f(x)在区间[-1,1)上的最大值为2…(4分)
(2)曲线y=f(x)上存在两点P、Q满足题设要求,则点P,Q只能在y轴的两侧,
不妨设P(t,f(t))(t>0),则Q(-t,t3+t2),显然t≠1.…(5分)
∵△POQ是以O为直角顶点的直角三角形,
∴$\overrightarrow{OP}•\overrightarrow{OQ}=0$,即-t2+f(t)(t3+t2)=0.(1)
是否存在两点P、Q等价于方程(1)是否有解.…(6分)
若0<t<1,则f(t)=-t3+t2,代入(1)式得,-t2+(-t3+t2)(t3+t2)=0,即t4-t2+1=0,
而此方程无实数解,因此t>1.…(8分)
∴f(t)=alnt,代入(1)式得,-t2+(alnt)(t3+t2)=0,即$\frac{1}{a}=(t+1)lnt$. (*)…(9分)
考察函数在h(x)=(x+1)lnx(x≥1),则$h'(x)=lnx+\frac{1}{x}+1>0$,
∴h(x)在[1,+∞)上单调递增,∵t>1,∴h(t)>h(1)=0,
当t→+∞时,h(t)→+∞,∴h(t)的取值范围是(0,+∞).…(11分)
∴对于a>0,方程(*)总有解,即方程(1)总有解.
因此对任意给定的正实数a,曲线y=f(x)上总存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.…(12分)
点评 本题考查导数知识的运用,考查学生分析解决问题的能力,考查学生的计算能力,综合性强,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
17.已知复数z满足(1+i)z=2i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
12.如图,正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值是( )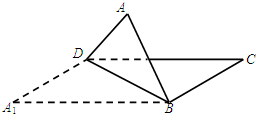

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |