题目内容
10.证明:lnx-$\frac{1}{4}$x2≤$\frac{\sqrt{2}}{4}$$\sqrt{{x}^{4}+1}$-$\frac{3}{4}$.分析 由基本不等式,可得$\sqrt{{x}^{4}+1}$≥$\sqrt{2{x}^{2}}$,要证原不等式成立,即证lnx-$\frac{1}{4}$x2≤$\frac{1}{2}$x-$\frac{3}{4}$,设f(x)=lnx-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$,x>0,求出导数,求得单调区间,求得极大值,且为最大值,即可得证.
解答 证明:∵$\sqrt{{x}^{4}+1}$≥$\sqrt{2{x}^{2}}$,
∴要证lnx-$\frac{1}{4}$x2≤$\frac{\sqrt{2}}{4}$$\sqrt{{x}^{4}+1}$-$\frac{3}{4}$,
即证lnx-$\frac{1}{4}$x2≤$\frac{1}{2}$x-$\frac{3}{4}$,
设f(x)=lnx-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$,x>0,
则f′(x)=$\frac{1}{x}$-$\frac{1}{2}$x-$\frac{1}{2}$=$\frac{2-x-{x}^{2}}{2x}$,x>0,
由f′(x)>0,得0<x<1;由f′(x)<0,得x>1,
∴x=1时,f(x)取得极大值,且为最大值f(1)=0,
即有f(x)=lnx-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$≤0,
即为lnx-$\frac{1}{4}$x2≤$\frac{1}{2}$x-$\frac{3}{4}$,
∴lnx-$\frac{1}{4}$x2≤$\frac{\sqrt{2}}{4}$$\sqrt{{x}^{4}+1}$-$\frac{3}{4}$.
点评 本题考查导数的运用:求极值和最值,考查不等式的证明方法:导数法,借助基本不等式,构造函数是解题的关键.

 名校课堂系列答案
名校课堂系列答案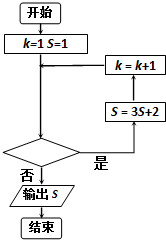
| A. | k<5? | B. | k>7? | C. | k≤5? | D. | k≤6? |
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深 | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上认为是安全的(船舶停靠时,船底只要不碰海底即可).某船吃水深度(船底离地面的距离)为6.5米.
Ⅰ)如果该船是旅游船,1:00进港希望在同一天内安全出港,它至多能在港内停留多长时间(忽略进出港所需时间)?
Ⅱ)如果该船是货船,在2:00开始卸货,吃水深度以每小时0.5米的速度减少,由于台风等天气原因该船必须在10:00之前离开该港口,为了使卸下的货物尽可能多而且能安全驶离该港口,那么该船在什么整点时刻必须停止卸货(忽略出港所需时间)?