题目内容
12.如图,正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值是( )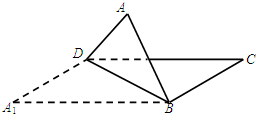
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由已知可得AO⊥平面BCD,则OC,OA,OD两两互相垂直,以O为原点,建立空间直角坐标系O-xyz,分别求出平面ACD和平面BCD的法向量,代入向量夹角公式,即可得到二面角A-CD-B的余弦值.
解答 解:∵正方形A1BCD的对角线BD为棱折成直二面角,
∴平面ABD⊥平面BCD,
连接BD,A1C,相交于O,
则AO⊥BD,
∵平面ABD∩平面BCD=BD,AO?平面ABD
∴AO⊥平面BCD,则OC,OA,OD两两互相垂直,
如图,以O为原点,建立空间直角坐标系O-xyz.
设正方形的棱长为1,
则O(0,0,0),A(0,0,$\frac{\sqrt{2}}{2}$),C($\frac{\sqrt{2}}{2}$,0,0),B(0,-$\frac{\sqrt{2}}{2}$,0),D(0,$\frac{\sqrt{2}}{2}$,0),
$\overrightarrow{OA}$=(0,0,$\frac{\sqrt{2}}{2}$)是平面BCD的一个法向量.
$\overrightarrow{AC}$=($\frac{\sqrt{2}}{2}$,0,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{BC}$=($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,0),$\overrightarrow{CD}$=(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,0)
设平面ACD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CD}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y=0}\\{\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}z=0}\end{array}\right.$,即$\left\{\begin{array}{l}{y=x}\\{z=x}\end{array}\right.$,
令x=1,则y=1,z=1,
解得$\overrightarrow{n}$=(1,1,1).
从而|cos<$\overrightarrow{n}$,$\overrightarrow{OA}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{OA}|}{|\overrightarrow{n}||\overrightarrow{OA}|}$=$\frac{|\frac{\sqrt{2}}{2}|}{\sqrt{3}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{3}}{3}$,
二面角A-CD-B的余弦值为$\frac{\sqrt{3}}{3}$,
故选:B
点评 本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,解答的关键是分别求出平面ACD和平面BCD的法向量,利用向量法是解决空间二面角大小的基本方法.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB. 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.