题目内容
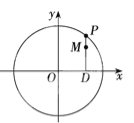
【题目】已知抛物线![]() 关于
关于![]() 轴对称,且经过点
轴对称,且经过点![]() .
.
(1)求抛物线![]() 的标准方程及其准线方程;
的标准方程及其准线方程;
(2)设![]() 为原点,过抛物线
为原点,过抛物线![]() 的焦点
的焦点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 交抛物线
交抛物线![]() 于两点
于两点![]() 、
、![]() ,抛物线的准线分别交直线
,抛物线的准线分别交直线![]() 、
、![]() 于点
于点![]() 和点
和点![]() ,求证:以
,求证:以![]() 为直径的圆经过
为直径的圆经过![]() 轴上的两个定点.
轴上的两个定点.
【答案】(1)标准方程为![]() ,准线方程为
,准线方程为![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)设抛物线C:x2=﹣2py,代入点(2,﹣1),解方程可得p,求得抛物线的方程和准线方程;(2)抛物线x2=﹣4y的焦点为F(0,﹣1),设直线方程为y=kx﹣1,联立抛物线方程,运用韦达定理,以及直线的斜率和方程,求得A,B的坐标,可得AB为直径的圆方程,可令x=0,解方程,即可得到所求定点.
(1)设抛物线C:x2=﹣2py,经过点(2,﹣1).可得4=2p,即p=2,
可得抛物线C的方程为x2=﹣4y,准线方程为y=1;
(2)抛物线x2=﹣4y的焦点为F(0,﹣1),
设直线方程为y=kx﹣1,联立抛物线方程,可得x2+4kx﹣4=0,
设M(x1,y1),N(x2,y2),
可得x1+x2=﹣4k,x1x2=﹣4,
直线OM的方程为y![]() x,即y
x,即y![]() x,
x,
直线ON的方程为y![]() x,即y
x,即y![]() x,
x,
可得A(﹣![]() ,1),B(﹣
,1),B(﹣![]() ,1),
,1),
可得AB的中点的横坐标为﹣2(![]() )=﹣2
)=﹣2![]() ﹣2k,
﹣2k,
即有AB为直径的圆心为(﹣2k, 1),
半径为![]() |
|![]() |=2
|=2![]() 2
2![]() ,
,
可得圆的方程为(x+2k)2+(y﹣1)2=4(1+k2),
化为x2+4kx+(y﹣1)2=4,
由x=0,可得y=﹣1或3.
则以AB为直径的圆经过y轴上的两个定点(0,﹣1),(0,3).

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |