题目内容
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在
,且在![]() 上是增函数,若
上是增函数,若![]() 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据f(x+2)=f(x),得函数的周期为2,在[﹣3,﹣2]上是减函数,可得f(x)在[﹣1,0]上为减函数,由f(x)为偶函数,得f(x)在[0,1]上为单调增函数.再根据α,β是锐角三角形的两个内角,利用三角函数诱导公式化简可得答案.
由题意:可知f(x+2)=f(x),
∴f(x)是周期为2的函数,
∵f(x)在[﹣3,﹣2]上为减函数,
∴f(x)在[﹣1,0]上为减函数,
又∵f(x)为偶函数,根据偶函数对称区间的单调性相反,
∴f(x)在[0,1]上为单调增函数.
∵在锐角三角形中,π﹣α﹣β![]()
∴π﹣α﹣β![]() ,即
,即![]() ,
,
∴![]() α
α![]() β>0,
β>0,
∴sinα>sin(![]() )=cosβ;
)=cosβ;
∵f(x)在[0,1]上为单调增函数.
所以f(sinα)>f(cosβ),
故选:D.

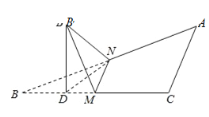
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
【题目】某二手交易市场对某型号的二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数x | 2 | 4 | 6 | 8 | 10 |
销售价格y | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程![]() .
.
(参考公式: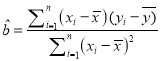 ,
,![]() )
)
(2)已知每辆该型号汽车的收购价格为ω=0.05x2﹣1.75x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,销售一辆该型号汽车所获得的利润z最大?(利润=销售价格﹣收购价格)
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() span>年至
span>年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
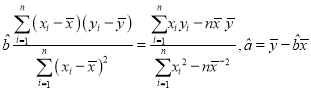 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)