题目内容
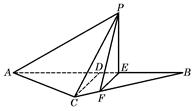
如图所示在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形。(12分)

(1)求PC和平面ABCD所成角的大小;
(2)求二面角B─AC─P的大小。

(1)求PC和平面ABCD所成角的大小;
(2)求二面角B─AC─P的大小。
⑴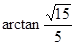 或者
或者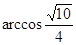 ⑵
⑵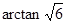 或者
或者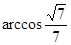
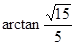 或者
或者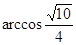 ⑵
⑵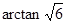 或者
或者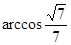
试题分析:(1)作
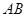 的中点
的中点 ,连接
,连接 ,
,因为△PAB为等边三角形,所以
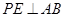 ,
,因为平面PAB⊥平面ABCD,所以PE⊥平面ABCD,
所以
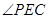 即为PC和平面ABCD所成角,
即为PC和平面ABCD所成角,因为底面ABCD是边长为2的正方形,
所以在
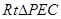 中,
中,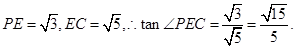
所以PC和平面ABCD所成角的大小为
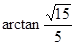 .
.(2)过E作
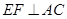 ,垂足为
,垂足为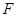 ,连接
,连接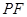 ,
,由(1)知
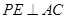 ,又
,又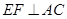 ,且
,且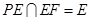 ,所以
,所以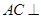 平面
平面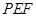 ,
,所以
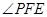 即为二面角B─AC─P的平面角.
即为二面角B─AC─P的平面角.在
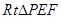 中,
中,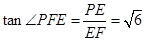 ,
,所以二面角B─AC─P的大小为
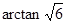 .
.点评:解决立体几何问题时,要充分发挥空间想象能力,紧扣相应的判定定理和性质定理,证明时要将定理所需要的条件一一列举出来,求角时要先作后证再求,还要注意角的取值范围.

练习册系列答案
相关题目
 ,
, 为
为 的中点,
的中点,
 为面
为面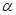 内的动点,且
内的动点,且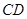 的距离为
的距离为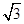 ,则
,则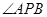 的最大值( )
的最大值( )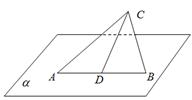

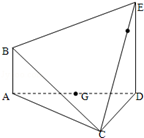

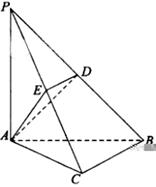
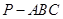 中,
中, ,
,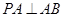 ,
,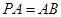 ,
,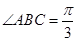 ,
,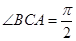 , 点
, 点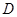 ,
, 分别在棱
分别在棱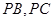 上,且
上,且 ,
,
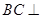 平面PAC
平面PAC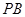 的中点时,求
的中点时,求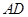 与平面
与平面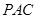 所成的角的正弦值;
所成的角的正弦值;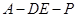 为直二面角?并说明理由.
为直二面角?并说明理由. 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。





 底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
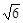 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记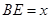 ,用
,用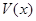 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.