题目内容
如图,在四棱锥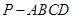 中,
中,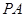 ⊥平面
⊥平面 ,
,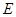 为
为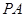 的中点,
的中点, 为
为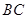 的中点,底面
的中点,底面 是菱形,对角线
是菱形,对角线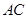 ,
, 交于点
交于点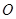 .
.
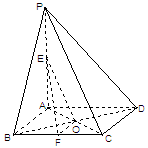
求证:(1)平面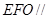 平面
平面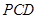 ;
;
(2)平面 ⊥平面
⊥平面 .
.
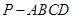 中,
中,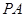 ⊥平面
⊥平面 ,
,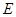 为
为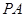 的中点,
的中点, 为
为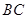 的中点,底面
的中点,底面 是菱形,对角线
是菱形,对角线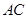 ,
, 交于点
交于点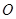 .
.
求证:(1)平面
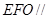 平面
平面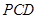 ;
;(2)平面
 ⊥平面
⊥平面 .
.(1)先利用线面平行的判定定理证明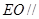 平面
平面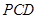 ,
,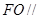 平面
平面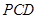 ,即得证
,即得证
(2)先利用线面垂直的判定定理证明 ⊥平面
⊥平面 ,即得证
,即得证
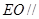 平面
平面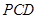 ,
,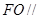 平面
平面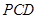 ,即得证
,即得证(2)先利用线面垂直的判定定理证明
 ⊥平面
⊥平面 ,即得证
,即得证试题分析:(1)因为
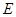 为
为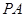 的中点,
的中点,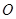 为
为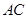 的中点,所以
的中点,所以
又
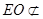 平面
平面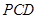 ,
, 平面
平面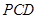 ,所以
,所以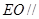 平面
平面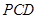 ……4分
……4分同理可证,
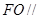 平面
平面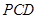 ,又
,又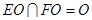
所以,平面
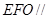 平面
平面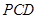 . ……7分
. ……7分(2)因为
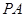 ⊥平面
⊥平面 ,
,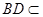 平面
平面 ,所以
,所以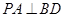 ……9分
……9分因为底面
 是菱形,所以
是菱形,所以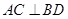 ,又
,又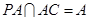
所以
 ⊥平面
⊥平面 ……12分
……12分又
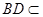 平面
平面 ,所以平面
,所以平面 ⊥平面
⊥平面 . ……14分
. ……14分点评:要解决此类问题,要充分发挥空间想象能力,紧扣相应的判定定理和性质定理,定理中要求的条件要一一列举出来,缺一不可.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 ,
, 为
为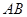 的中点,
的中点,
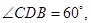
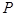 为面
为面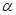 内的动点,且
内的动点,且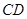 的距离为
的距离为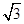 ,则
,则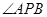 的最大值( )
的最大值( )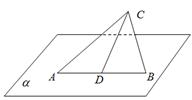

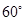
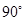
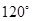
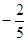
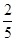
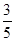
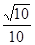
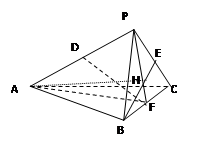
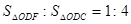
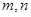 为两条不同的直线,
为两条不同的直线,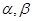 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是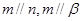 ,则
,则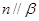
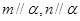 ,则
,则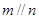
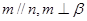 ,则
,则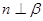
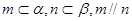 ,则
,则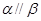
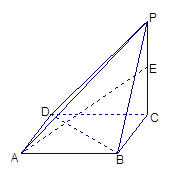
 中,
中, ,
,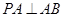 ,
,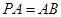 ,
,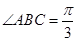 ,
,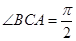 , 点
, 点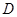 ,
, 分别在棱
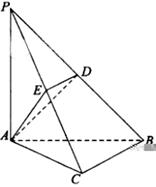
分别在棱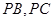 上,且
上,且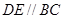 ,
,
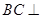 平面PAC
平面PAC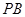 的中点时,求
的中点时,求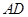 与平面
与平面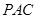 所成的角的正弦值;
所成的角的正弦值;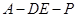 为直二面角?并说明理由.
为直二面角?并说明理由.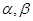 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
 ,则n∥
,则n∥