Question

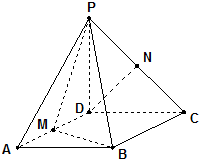
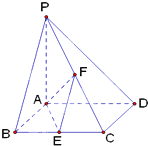
如图，已知四棱锥P-ABCD底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（1）证明：AE⊥PD；
（2）设AB=2，若H为线段PD上的动点，EH与平面PAD所成的最大角的正切值为

6

2

，求此时异面直线AE和CH所成的角．

Answer 1

（1）证明：∵四边形ABCD为棱形，∠ABC=60°，
∴△ABC是等边三角形，
∵E是BC的中点，∴AE⊥BC，
又∵BC∥AD，∴AE⊥AD，
∵PA⊥平面ABCD，AE?平面ABCD，∴PA⊥AE，
∵PA?平面PAD，AD?平面PAD，且PA∩AD=A，
∴AE⊥平面PAD，
又∵PD?平面PAD，∴AE⊥PD．
（2）设AB=2，H为PD上任意一点，
连接AH，EH，由（1）知AE⊥平面PAD，
∴∠EHA为EH与平面PAD所成的角，
在Rt△EAH中，AE=

3

，所以当AH最短时，即AH⊥PD时，EH与平面PAD所成的角∠EHA最大，
此时tan∠EHA=l
因此AH=AC₁∥面CDB₁．又AD=2，所以∠ADH=45°，所以PA=2．
此时异面直线AE和CH异面直线所成角30°．