题目内容

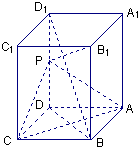
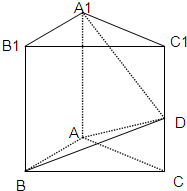
直三棱柱ABC-A1B1C1的底面中，AB⊥AC，AB=AC=a，D为CC1的中点，
CC1
AC
=λ
（1）λ为何值时，A1D⊥平面ABD；
（2）当A1D⊥平面ABD时，求C1到平面ABD的距离；
（3）当二面角A-BD-C为60°时，求λ的值．
以
AB
，
AC
，
AA1
为正交基底建立空间直角坐标系，
则A(0，0，0)，B(a，0，0)，C(0，a，0)，C1(0，a，λa)，D(0，a，
1
2
λa)，A1（0，0，λa）
（1）
A1D
=(0，a，-
λa
2
)，
AD
=(0，a，
λa
2
)
∵A1D⊥平面ABD∴A1D⊥AD
∴0+a2-
λ2a2
4
=0有λ=2
（2）λ=2时，
C1D
=(0，0，-a)，
A1D
=（0，a，-a）
∴C1到平面ABD的距离d=|
C1D
•
A1D
|
A1D
|
|=
2
2
a
（3）取BC中点E，连接AE，则AE⊥BC，又BB1⊥AE∴AE⊥平面BCD
AE
=(
a
2
，
a
2
，0)，设
m
=(x，y，z)为平面ABD的一个法向量
由
m
•
AB
=0
m
•
AD
=0
得
x=0
y=-
λz
2

取z=1得
m
=(0，-
λ
2
，1)，由cos60°=|
m
•
AE
|
m
|•|
AE
|
|得λ=2
练习册系列答案
相关题目
如图是一个长方体截去一个角所得的多面体的直观图及它的正（主）视图和侧（左）视图（单位：cm）．
（1）画出该多面体的俯视图；
（2）按照给出的尺寸，求该多面体的体积；
（3）在所给直观图中连接BC'，证明：BC'∥平面EFG．
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，DC∥AB，∠BAD=90°，且AB=2AD=2DC=2PD=4（单位：cm），E为PA的中点．
（1）证明：DE∥平面PBC；
（2）证明：DE⊥平面PAB．
正方体ABCD-A1B1C1D1中，E，F分别是棱AA1，BB1的中点．
（1）求证：平面A1BC1∥平面ACD1；
（2）求异面直线A1F与D1E所成的角的余弦值．
如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．
（1）求证：直线BD1∥平面PAC；
（2）求证：平面PAC⊥平面BDD1；
（3）求证：直线PB1⊥平面PAC．
已知直线l⊥平面α，有以下几个判断：
①若m⊥l，则m∥α，
②若m⊥α，则m∥l
③若m∥α，则m⊥l，
④若m∥l，则m⊥α，
上述判断中正确的是（　　）
A．①②③B．②③④C．①③④D．①②④
已知四边形ABCD中，∠B=∠D=90°，AD=CD=
6
，∠BAC=60°，E为AC的中点；现将△ACD沿对角线AC折起，使点D在平面ABC上的射影H落在BC上．
（1）求证：AB⊥平面BCD；
（2）求三棱锥D-ABE的体积．
如图，已知四棱锥P-ABCD底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（1）证明：AE⊥PD；
（2）设AB=2，若H为线段PD上的动点，EH与平面PAD所成的最大角的正切值为
6
2
，求此时异面直线AE和CH所成的角．
如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证AE⊥平面BCE；
（Ⅱ）求二面角B-AC-E的大小；
（Ⅲ）求点D到平面ACE的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网