题目内容

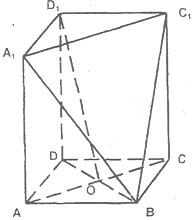
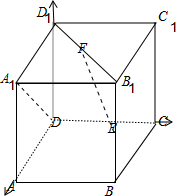
如图，ABCD-A1B1C1D1是正方体，点E，F分别是BB1，B1D1中点，求证：EF⊥DA1．
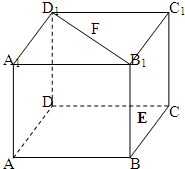
以
DA
，
DC
，
DD1
分别为x轴，y轴，z轴建立空间直角坐标系，如下图所示：
设正方体棱长为1，则A1（1，0，1），D（0，0，0），F（
1
2
，
1
2
，1），E（1，1，
1
2
），
所以
DA1
=（1，0，1），
EF
=（-
1
2
，-
1
2
，
1
2
），
因为
DA1
•
EF
=（1，0，1）•（-
1
2
，-
1
2
，
1
2
）=-
1
2
+0+
1
2
=0，
所以
DA1
⊥
EF
，即EF⊥DA1．
练习册系列答案
相关题目
在长方体ABCD-A1B1C1D1中，AB=BC=2，O为AC和BD的交点，过A、C1、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-AC1Dl，且这个几何体的体积为．
（1）求证：OD1∥平面BA1C1
（2）求棱A1A的长：
（3）求点D1到平面BA1C1的距离．
已知直线l⊥平面α，有以下几个判断：
①若m⊥l，则m∥α，
②若m⊥α，则m∥l
③若m∥α，则m⊥l，
④若m∥l，则m⊥α，
上述判断中正确的是（　　）
A．①②③B．②③④C．①③④D．①②④
如图所示，在四棱锥P-ABCD中，底面四边形ABCD是正方形，PD⊥平面ABCD，E为PC的中点．
求证：
（1）PA∥平面BDE；
（2）AC⊥平面PBD．
如图，已知四棱锥P-ABCD底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（1）证明：AE⊥PD；
（2）设AB=2，若H为线段PD上的动点，EH与平面PAD所成的最大角的正切值为
6
2
，求此时异面直线AE和CH所成的角．
如图，正三棱柱ABC-A1B1C1的各棱长都为m，E是侧棱CC1的中点，求证AB1⊥平面A1BE．
如图，在三棱柱ABC-A1B1C1中，AB⊥侧面BB1C1C，已知BB1=2，AB=
2
，BC=1，∠BCC1=
π
3

（1）求证：C1B⊥平面ABC；
（2）试在棱CC1（不包含端点C，C1）上确定一点E的位置，使得EA⊥EB1．
如图，在长方体ABCD-A1B1C1D1中，底面ABCD是正方形，E是DD1的中点．
（1）求证：AC⊥B1D；
（2）若B1D⊥平面ACE，求
AA1
AB
的值．
如图，已知三棱锥P-ABC的侧面PAB是等边三角形，D是AB的中点，PC=BC=AC=2，PB=2
2
．
（1）证明：AB⊥平面PCD；
（2）求点C到平面PAB的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网