Question

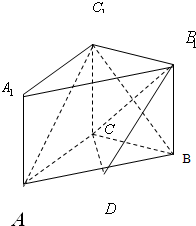
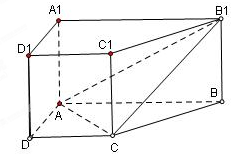
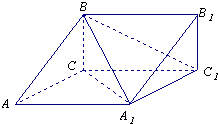
如图，三棱柱ABC-A₁B₁C₁中，∠CAA₁=60°，AA₁=2AC，BC⊥平面AA₁C₁C．
（1）证明：A₁C⊥AB；
（2）设BC=AC=2，求三棱锥C-A₁BC₁的体积．

Answer 1

（1）证明：在△ACA₁中，
由余弦定理得A1C2=AC2+AA12-2AC•AA1cos60°=3AC²，
∴A1C=

3

AC，
∴AC2+A1C2=A1A2，∴∠ACA1=90°，∴A₁C⊥AC．
∵BC⊥平面AA₁C₁C，∴BC⊥A₁C．
∵AC∩BC=C，∴A₁C⊥平面ABC，∴A₁C⊥AB．
（2）作A₁E⊥CC₁，CF⊥AA₁．
则A₁E⊥平面BCC₁B₁，四边形A₁ECF为矩形．
在Rt△ACF中，CF=ACsin60°=

3

．
S△BCC1=

1

2

×4×2=4，
∴V三棱锥C-A1C1B=V三棱锥A1-BCC1=

1

3

×4×

3

=

4 3

3

．