题目内容
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
【答案】(1) ![]() 是“局部奇函数”,理由见解析;(2)
是“局部奇函数”,理由见解析;(2) ![]() ;(3)
;(3) ![]()
【解析】试题分析:
(1)结合函数的解析式,当![]() 或
或![]() 时,
时, ![]() 成立,则
成立,则![]() 是“局部奇函数”;
是“局部奇函数”;
(2)由题意换元令![]() 结合对勾函数的性质可得
结合对勾函数的性质可得![]()
(3)由定义得![]() 有解,结合函数的性质分类讨论:①若
有解,结合函数的性质分类讨论:①若![]() 则
则![]()
②若![]() 则
则![]()
故实数![]() 的取值范围是
的取值范围是![]()
试题解析:
(1)由题意得: ![]()
当![]() 或
或![]() 时,
时, ![]() 成立,
成立, ![]() 是“局部奇函数”;
是“局部奇函数”;
(2)由题意得: ![]()
![]() 在
在![]() 有解,
有解, ![]()
令![]() 则
则![]() 设
设![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增
单调递增![]()
(3)由定义得![]()
即![]() 有解,
有解,
设![]() 方程等价于
方程等价于![]() 在
在![]() 时有解,
时有解,
设![]() 对称轴
对称轴![]()
①若![]() 则
则![]() 即
即![]() 此时
此时![]()
②若![]() 则
则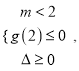 即
即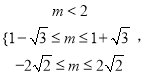 此时
此时![]()
综上得: ![]() 即实数
即实数![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)