题目内容
7.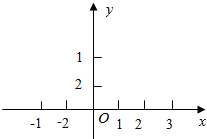 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.(1)求f(f(0))的值;
(2)在给出坐标系中画出函数f(x)的大致图象(只画图象不写过程).
分析 (1)根据函数的解析式求得f(0)的值,从而求得f[f(0)]的值.
(2)根据函数的解析式做出函数f(x)的图象.
解答  解:(1)∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$,
解:(1)∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$,
∴f(0)=1,
∴f(f(0))=f(1)=0.
(2)函数f(x)的图象如图所示:
点评 本题主要考查求函数的值,做函数的图象,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
17.在等差数列{an}中,Sn为其前n项和,若a3=8,则S5=( )
| A. | 16 | B. | 24 | C. | 32 | D. | 40 |
15.用1,2,3,4排成数字不重复的四位数,若已知1、2相邻,则1、3相邻的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
2.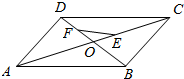 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )| A. | $\overrightarrow{FE}$=-$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | B. | $\overrightarrow{FE}$=$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | C. | $\overrightarrow{FE}$=$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ | D. | $\overrightarrow{FE}$=-$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ |
16.若$sinα=-\frac{5}{13},且α$为第四象限角,则$tan({α+\frac{π}{4}})$的值等于( )
| A. | $\frac{7}{17}$ | B. | $\frac{17}{7}$ | C. | $-\frac{5}{12}$ | D. | $\frac{10}{17}$ |
17.以双曲线$\frac{x^2}{4}-{y^2}=1$的中心为顶点,右焦点为焦点的抛物线方程是( )
| A. | y2=4x | B. | ${y^2}=4\sqrt{5}x$ | C. | ${y^2}=8\sqrt{5}x$ | D. | ${y^2}=\sqrt{5}x$ |