题目内容
14.设函数f(x)=$\frac{1}{3}{x}^{3}$-ax2-ax,g(x)=2x2+4x+c(Ⅰ)试问函数f(x)能否在x=-1时取得极值?说明理由;
(Ⅱ)若a=-1,当x∈[-3,4]时,方程f(x)=g(x)有二个不等实根,求c的取值范围.
分析 (Ⅰ)先求出函数f(x)的导数,先假设存在极值,得出矛盾即可;
(Ⅱ)问题转化为c=$\frac{1}{3}$x3-x2-3x有2个不等实根,设F(x)=$\frac{1}{3}$x3-x2-3x,G(x)=c,通过求导得到函数f(x)的最值,从而判断出c的范围.
解答 解:(Ⅰ)由题意f′(x)=x2-2ax-a,
假设在x=-1时f(x)取得极值,则有f′(-1)=1+2a-a=0,∴a=-1,
而此时,f′(x)=(x+1)2≥0,函数f(x)在x=-1处无极值;
(Ⅱ)f(x)=g(x),则有$\frac{1}{3}$x3-x2-3x-c=0,
∴c=$\frac{1}{3}$x3-x2-3x,
设F(x)=$\frac{1}{3}$x3-x2-3x,G(x)=c,
令F′(x)=x2-2x-3=0,解得x=-1或x=3,
列表如下:
| x | -3 | (-3,-1) | -1 | (-1,3) | 3 | (3,4) | 4 |
| F′(x) | + | 0 | - | 0 | + | ||
| F(x) | -9 | 增 | $\frac{5}{3}$ | 减 | -9 | 增 | -$\frac{20}{3}$ |
当x=-1时,F(x)取得极大值F(-1)=$\frac{5}{3}$;当x=3时,F(x)取得极小值,
F(-3)=F(3)=-9,而F(4)=-$\frac{20}{3}$,
所以-$\frac{20}{3}$<c<$\frac{5}{3}$或c=-9.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数的交点问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在等差数列{an}中,已知a2+a3+a4=18,那么s5=( )
| A. | 30 | B. | 35 | C. | 18 | D. | 26 |
9.等差数列{an}的前n项和为Sn,已知a1=-12,S13=0,使得an>0的最小正整数n等于( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 (
( 为常数,
为常数,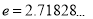 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与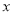 轴平行.
轴平行.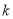 的值;
的值; 的单调区间;
的单调区间; ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 ,
,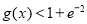 .
. 在函数
在函数 的图象上,则
的图象上,则 的值为( )
的值为( ) B.
B. C.1 D.
C.1 D.