题目内容
2.在等差数列{an}中,已知a2+a3+a4=18,那么s5=( )| A. | 30 | B. | 35 | C. | 18 | D. | 26 |
分析 根据等差数列的性质以及前n项和公式进行求解即可.
解答 解:∵a2+a3+a4=18,
∴3a3=18,即a3=6,
则s5=$\frac{5({a}_{1}+{a}_{5})}{2}$=$\frac{5×2{a}_{3}}{2}$=5a3=5×6=30,
故选:A.
点评 本题主要考查等差数列前n项和公式的计算,根据等差数列的性质求出a3=6是解决本题的关键.

练习册系列答案
相关题目
13.sin1290°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
17.在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)的值为( )
| A. | 4 | B. | 10 | C. | 20 | D. | 40 |
 满足
满足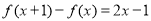 ,且
,且 .
. 的解析式;
的解析式; 时,
时,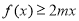 恒成立,求实数
恒成立,求实数 的取值集合.
的取值集合. 如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.
如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.