题目内容
19.若实数x,y满足$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥1}\end{array}\right.$,且S=2x+y-2,则S的最大值为( )| A. | 5 | B. | 3 | C. | 2 | D. | 1 |
分析 画出约束条件表示的可行域,确定目标函数经过的特殊点,求出最大值即可
解答  解:约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥1}\end{array}\right.$,表示的可行域如图阴影部分,
解:约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥1}\end{array}\right.$,表示的可行域如图阴影部分,
目标函数S=2x+y-1经过可行域A点,即$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$的交点坐标(2,3)
目标函数时取得最大值,
最大值为:2×2+3-2=5.
故选:A.
点评 本题考查约束条件表示的可行域的画法,特殊点的确定是解题的关键,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.等差数列{an}的前n项和为Sn,若a7的值为常数,则下列各数中也是常数的是( )
| A. | S7 | B. | S8 | C. | S13 | D. | S15 |
4.根据下列算法语句,当输入x为6时,输出y的值为( )
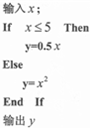
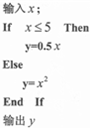
| A. | 25 | B. | 30 | C. | 36 | D. | 61 |
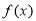 满足
满足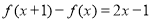 ,且
,且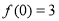 .
.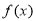 的解析式;
的解析式;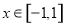 时,
时,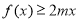 恒成立,求实数
恒成立,求实数 的取值集合.
的取值集合.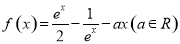 .
.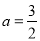 时,求函数
时,求函数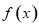 的单调区间;
的单调区间;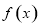 在
在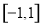 上为单调函数,求实数
上为单调函数,求实数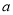 的取值范围.
的取值范围.