题目内容
若不等式x>0,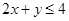 与
与 所确定的平面区域被直线
所确定的平面区域被直线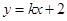 分为面积相等的两部分,则k的值是( )
分为面积相等的两部分,则k的值是( )
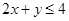 与
与 所确定的平面区域被直线
所确定的平面区域被直线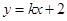 分为面积相等的两部分,则k的值是( )
分为面积相等的两部分,则k的值是( )| A.1 | B. 2 | C.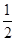 | D.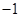 |
A
分析:先画出不等式组
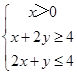 所表示的平面区域,求出平面区域的面积以及在直线y="kx+2" 一侧的面积;再结合平面区域被直线y="kx+2" 分为面积相等的两部分即可求出k的值.
所表示的平面区域,求出平面区域的面积以及在直线y="kx+2" 一侧的面积;再结合平面区域被直线y="kx+2" 分为面积相等的两部分即可求出k的值.解:不等式组
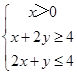 所表示的平面区域为三角形ABC.
所表示的平面区域为三角形ABC.由
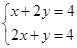 ?
?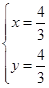 .故点C(
.故点C(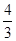 ,
,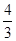 ).
).由
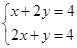 ?
?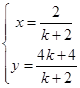 ,故点D(
,故点D(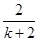 ,
, )
)所以 S△ABD=
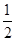 ×|AB|?xD=
×|AB|?xD=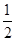 x2×
x2×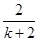 =
=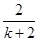 .
.S△ABC=
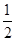 ×|AB|?xC=
×|AB|?xC=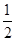 ×2×
×2×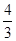 =
=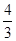 .
.又因为平面区域被直线y="kx+2" 分为面积相等的两部分
∴S△ABD=
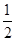 S△ABC即
S△ABC即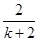 =
=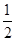 ×
×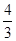 ,解得k=1.
,解得k=1.故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为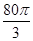 立方米,且
立方米,且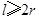 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为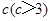 .设该容器的建造费用为
.设该容器的建造费用为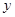 千元.
千元.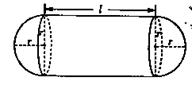
 关于
关于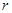 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;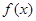 在定义域R内可导,若
在定义域R内可导,若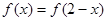 ,且当
,且当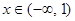 时,
时,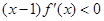 ,设
,设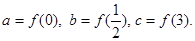 则( )
则( )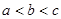
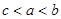
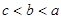

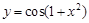 的导数是( )
的导数是( ) B.
B.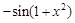 C.
C. D.
D.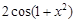
 中任取的一个数,
中任取的一个数,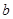 为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线
为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线 交点处的切线相互平行的概率是
交点处的切线相互平行的概率是
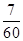
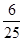
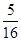
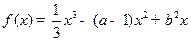 ,其中
,其中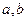 为常数.
为常数.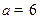 ,
,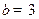 时,求函数
时,求函数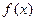 的单调递增区间;
的单调递增区间;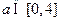 ,
,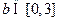 ,求函数
,求函数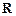 上是增函数的概率.
上是增函数的概率.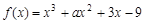 ,已知
,已知 在
在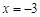 时取极值,则a=
时取极值,则a=