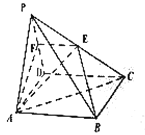
题目内容
【题目】制订投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测，甲、乙项目可能的最大盈利分别为
和
，可能的最大亏损率分别为
和
.投资人计划投资金额不超过
亿元，要求确保可能的资金亏损不超过
亿元，问投资人对甲、乙两个项目各投资多少亿元，才能使可能的盈利最大？
【答案】投资人用
亿元投资甲项目，
亿元投资乙项目，才能在确保亏损不超过
亿元的前提下，使可能的盈利最大.
【解析】
设投资人分别用
亿元、
亿元投资甲、乙两个项目，根据题意列出变量、所满足的约束条件和线性目标函数，利用平移直线的方法得出线性目标函数取得最大值时的最优解，并将最优解代入线性目标函数可得出盈利的最大值，从而解答该问题.
设投资人分别用亿元、亿元投资甲、乙两个项目，
由题意知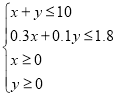
，即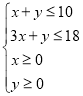
，目标函数为
.
上述不等式组表示平面区域如图所示，阴影部分（含边界）即可行域.
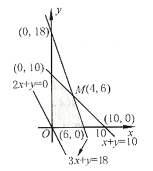
由图可知，当直线经过点
时，该直线在轴上截距最大，此时
取得最大值，解方程组
，得
，所以，点的坐标为
.
当
，
时，取得最大值，此时，
（亿元）.
答：投资人用亿元投资甲项目，亿元投资乙项目，才能在确保亏损不超过亿元的前提下，使可能的盈利最大.
练习册系列答案
相关题目
