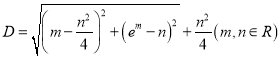题目内容
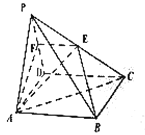
【题目】如图,在四棱锥![]() 中,
中,![]() 为棱
为棱![]() 中点,底面
中点,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() 为正三角形,平面
为正三角形,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,平面
,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)求四棱锥![]() 的表面积.
的表面积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据直线与平面平行的判定定理得![]() 面
面![]() ,根据直线与平面平行的性质定理得
,根据直线与平面平行的性质定理得![]() ,同理
,同理![]() ,再根据平行公理4可证
,再根据平行公理4可证![]() ,
,
(2)利用三角形的面积公式和直角梯形的面积公式计算五个面的面积再相加即可得到答案.
解:(1)如图所示:
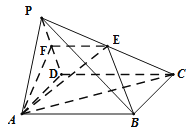
∵![]() 为正方形,∴
为正方形,∴![]() ,
,
∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
∵![]() 为
为![]() 中点,平面
中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,∴面
,∴面![]() 面
面![]() ,
,
∴![]() .
.
同理![]() ,∴
,∴![]() .
.
(2)由(1)知![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
又∵![]() 为
为![]() 中点,∴
中点,∴![]() 为
为![]() 中点,且
中点,且![]() ,
,
又∵![]() 正三角形,且边长为2,∴
正三角形,且边长为2,∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 为正方形,∴
为正方形,∴![]() ,
,
又∵面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() 为直角梯形,
为直角梯形,
∴![]() .
.
∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() .
.
∴![]() .
.
同理![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
同理![]() ,
,
又∵![]() ,∴
,∴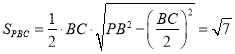 ,
,
又∵![]() 为
为![]() 中点,∴
中点,∴![]() .
.
∴四棱锥![]() 的表面积
的表面积![]()
![]() .
.

练习册系列答案
相关题目