题目内容
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
分析 由数列递推式构造等比数列{an+1},求其通项公式后可得数列{an}的通项公式.
解答 解:由an+1=4an+3(n∈N*),得an+1+1=4(an+1),
∵a1=3,∴a1+1=3+1=4≠0,
则数列{an+1}是以4为首项,以4为公比的等比数列,
∴${a}_{n}+1=4×{4}^{n-1}={4}^{n}={2}^{2n}$,
则${a}_{n}={2}^{2n}-1$.
故选:D.
点评 本题考查了数列递推式,考查了构造等比数列求数列的通项公式,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.2014巴西世界杯结束后,某网站针对世界杯情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定;观看世界杯直播32场(含)以下者,称为“非球迷”,观看比赛直播超过32场这成为“球迷”,得到如下统计表:
若参与调查的“非球迷”总人数为7600人.
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
5.设m,n是两条不同的直线,α,β是两个不同的平面,则( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
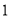 ,
,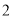 ,
,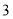 ,
,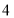 的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为
的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为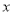 ,
,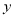 .
.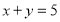 的概率;
的概率;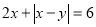 的概率.
的概率.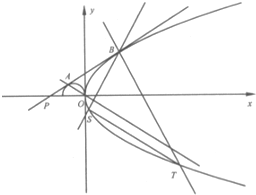 已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.
已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.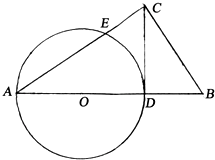 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.