题目内容
4.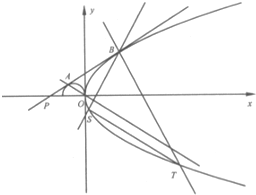 已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.
已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.(1)求抛物线C的方程及点A,B的坐标;
(2)过点B作倾斜角互补的两条直线分别交抛物线C于S,T两点(不同于坐标原点O),求证:直线ST∥直线AO.
分析 (1)通过直线l与半圆M相切可得圆心到直线l的距离为1,可得直线l的斜率,联立直线l与抛物线C的方程,利用韦达定理计算即得结论;
(2)设直线BS、BT的两条直线斜率分别为t,-t,分别联立直线BS、BT与抛物线方程,利用韦达定理B、T点纵坐标,根据斜率公式计算即可.
解答 (1)解:半圆M方程化为:(x+1)2+y2=1(y≥0),
设l的方程为y=k(x+3),即kx-y+3k=0,
由题意得得k>0,又dM-l=$\frac{|-k+3k|}{\sqrt{1+{k}^{2}}}$=1,解得k=$\frac{\sqrt{3}}{3}$,
故l的方程为y=$\frac{\sqrt{3}}{3}$(x+3),
代入抛物线C:y2=2px(p>0)方程,得x2+(6-6p)x+9=0,
由△=(6-6p)2-36=0,得p=2,
进而得B(3,2$\sqrt{3}$),
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}(x+3)}\\{{x}^{2}+2x+{y}^{2}=0(y>0)}\end{array}\right.$,解得A(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
故抛物线C的方程为:y2=4x,点A坐标为A(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),点B坐标为B(3,2$\sqrt{3}$);
(2)证明:设直线BS、BT的两条直线斜率分别为t,-t,
则直线BS为:y-2$\sqrt{3}$=t(x-3),代入抛物线方程y2=4x,
消去x得:ty2-4y+8$\sqrt{3}$-12t=0,
由韦达定理可得yB+yS=$\frac{4}{t}$,
∴yS=$\frac{4}{t}$-2$\sqrt{3}$,同理可得yT=-$\frac{4}{t}$-2$\sqrt{3}$,
∴kST=$\frac{{y}_{S}-{y}_{T}}{{x}_{S}-{x}_{T}}$=$\frac{{y}_{S}-{y}_{T}}{\frac{{{y}_{S}}^{2}-{{y}_{T}}^{2}}{4}}$=$\frac{4}{{y}_{S}-{y}_{T}}$=$\frac{4}{-4\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$,
由(1)知A(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),∴kAO=-$\frac{\sqrt{3}}{3}$,即kST=kAO,
又两直线直线ST与直线AO不重合,
∴直线ST∥直线AO.
点评 本题是一道直线与圆锥曲线的综合题,涉及韦达定理、斜率计算公式等知识,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
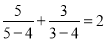 ,
,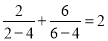 ,
,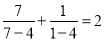 ,
,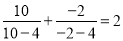 ,依照以上各式成立的规律,得到一般性的等式为( )
,依照以上各式成立的规律,得到一般性的等式为( )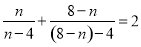 B.
B.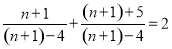
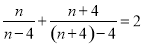 D.
D.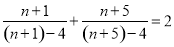
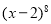 的展开式中,
的展开式中,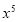 的系数为______.
的系数为______.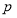 :若
:若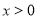 ,则函数
,则函数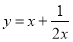 的最小值为
的最小值为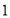 ;命题
;命题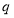 :若
:若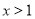 ,则
,则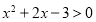 .则
.则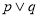 B.
B.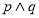
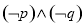 D.
D.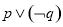
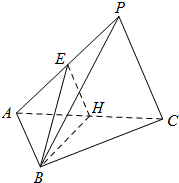 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.