题目内容
1.已知a>0,且a≠1函数f(x)=loga(1-ax)(1)求函数f(x)的定义域,判断并证明f(x)的单调性
(2)当a=e(e为自然对数的底数)时,设h(x)=(1-ef(x))(x2-m+1),若函数h(x)的极值存在,求实数m的取值范围以及函数h(x)的极值.
分析 (1)据对数函数的真数大于0,列出不等式求出定义域;求出导函数,利用导函数大于0函数得到递增;导函数小于0函数单调递减.
(2)求出导函数,令导函数为0,导函数是否有根进行分类讨论;导函数的根是否在定义域内再一次引起分类讨论,利用极值的定义求出极值.
解答 解:(1)由题意知,1-ax>0
所以当0<a<1时,f(x)的定义域是(0,+∞),a>1时,f(x)的定义域是(-∞,0),
f′(x)=$\frac{-{a}^{x}lna}{1-{a}^{x}}•lo{g}_{a}e$=$\frac{{a}^{x}}{{a}^{x}-1}$
当0<a<1时,x∈(0,+∞),因为ax-1<0,ax>0,故f'(x)<0,所以f(x)是减函数.
当a>1时,x∈(-∞,0),因为ax-1<0,ax>0,故f'(x)<0,所以f(x)是减函数;
(2)h(x)=ex(x2-m+1)(x<0),所以h'(x)=ex(x2+2x-m+1),
令h'(x)=0,即x2+2x-m+1=0,由题意应有△≥0,即m≥0.
①当m=0时,h'(x)=0有实根x=-1,在x=-1点左右两侧均有h'(x)>0,故h(x)无极值.
②当0<m<1时,h'(x)=0有两个实根x1=-1-$\sqrt{m}$,x2=-1+$\sqrt{m}$.
当x变化时,h'(x)的变化情况如下表:
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,0) |
| h′(x) | + | 0 | - | 0 | + |
| h(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
③当m≥1时,h'(x)=0在定义域内有一个实根x=-1-$\sqrt{m}$.
同上可得h(x)的极大值为$2{e}^{-1-\sqrt{m}}$(1+$\sqrt{m}$).
综上所述,m∈(0,+∞)时,函数h(x)有极值.
当0<m<1时,h(x)的极大值为$2{e}^{-1-\sqrt{m}}$(1+$\sqrt{m}$),h(x)的极小值为2${e}^{-1+\sqrt{m}}$(1-$\sqrt{m}$).
当m≥1时,h(x)的极大值为$2{e}^{-1-\sqrt{m}}$(1+$\sqrt{m}$).
点评 本题考查利用导数的符号讨论函数的单调性;利用导数研究函数的极值;在含参数的函数中需要分类讨论.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )
| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
16. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 |
 的展开式中,
的展开式中, 的系数为______.
的系数为______. 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$. 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
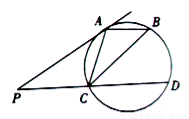
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.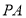 与圆切于点
与圆切于点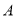 ,过
,过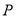 作直线与圆交于
作直线与圆交于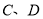 两点,点
两点,点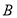 在圆上,且
在圆上,且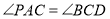 .
.
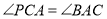 ;
;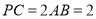 ,求
,求 .
.