题目内容
15.若不等式32x-k•3x+4≥0对于任意x∈R恒成立,求实数k的取值范围.分析 令t=3x(t>0),运用参数分离可得k≤t+$\frac{4}{t}$的最小值,运用基本不等式可得最小值,即可得到k的范围.
解答 解:令t=3x(t>0),不等式32x-k•3x+4≥0对于任意x∈R恒成立,
即为t2-kt+4≥0(t>0)恒成立,
即有k≤t+$\frac{4}{t}$的最小值,
由t+$\frac{4}{t}$≥2$\sqrt{t•\frac{4}{t}}$=4,当且仅当t=2取得最小值4.
则有k≤4.
即k的取值范围是(-∞,4].
点评 本题考查函数的恒成立问题的解法,注意运用换元法和指数函数的值域,由参数分离和基本不等式可得最小值,考查运算能力,属于中档题.

练习册系列答案
相关题目
 如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.
如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.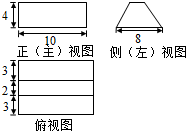 某几何体的三视图如图所示.则该几何体的体积为200.
某几何体的三视图如图所示.则该几何体的体积为200.