题目内容
7.等比数列{an}中,S10=10,S20=40,则S30=( )| A. | 70 | B. | 90 | C. | 130 | D. | 160 |
分析 根据等比数列的前n项和的性质进行求解.
解答 解:∵S10=10≠0,S20=40≠0,
∴由等比数列的性质可得S10,S20-S10,S30-S20仍成等比数列,
即10,30,S30-40成等比数列,
∴302=10(S30-40),
解得S30=130,
故选:C
点评 本题考查等比数列的性质,利用Sn,S2n-Sn,S3n-S2n仍成等比数列是解决问题的关键,属中档题.

练习册系列答案
相关题目
20.已知X和Y是两个分类变量,由公式K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$算出K2的观测值k约为7.822根据下面的临界值表可推断( )
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 推断“分类变量X和Y没有关系”犯错误的概率上界为0.010 | |
| B. | 推断“分类变量X和Y有关系”犯错误的概率上界为0.010 | |
| C. | 有至少99%的把握认为分类变量X和Y没有关系 | |
| D. | 有至多99%的把握认为分类变量X和Y有关系 |
16.袋中装有6只白球,5只黄球,4只红球,从中任取一球,抽到不是白球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{3}{5}$ | D. | .非以上答案 |
19.已知△ABC的三边长分别为a,b,c,若(b+c+a)(b+c-a)=3bc,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 ,集合
,集合 .
. ;
;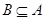 ,求实数
,求实数 的取值范围.
的取值范围.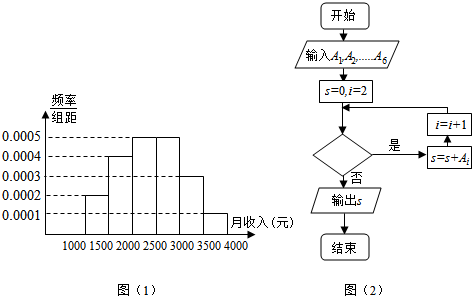
 某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示:
某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示: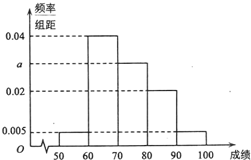 某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].