题目内容
1.袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色,现从袋中随机抽取3个小球.设每个小球被抽到的机会均等,则抽到白球或黑球的概率为( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{9}{10}$ |
分析 从口袋中5个小球中随机摸出3个小球,共有10种选法,则既没有黑球也没有白球只有1种,根据互斥事件的概率公式计算即可.
解答 解:从口袋中5个小球中随机摸出3个小球,共有C53=10种选法,则既没有黑球也没有白球只有1种,
∴每个小球被抽到的机会均等,则抽到白球或黑球的概率为1-$\frac{1}{10}$=$\frac{9}{10}$,
故选:D.
点评 本题考查了古典概型的概率计算公式和组合数的计算公式,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的概率等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
9.某班主任对全班50名学生进行了作业量多少的调查,数据如下:
则认为喜欢玩手机与认为作业多少有关系的把握大约为95%.
附:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当x2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当x2>2.706时,有90%的把握判定变量A,B有关联;
当x2>3.841时,有95%的把握判定变量A,B有关联;
当x2>6.635时,有99%的把握判定变量A,B有关联.
| 认为作业多 | 认为作业不多 | |
| 喜欢玩手机 | 18 | 9 |
| 不喜欢玩手机 | 7 | 16 |
附:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当x2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当x2>2.706时,有90%的把握判定变量A,B有关联;
当x2>3.841时,有95%的把握判定变量A,B有关联;
当x2>6.635时,有99%的把握判定变量A,B有关联.
6.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$,则a2015=( )
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
9.下列四个函数中,在区间(0,$\frac{1}{4}$)上为减函数的是( )
| A. | y=x($\frac{1}{2}$)x | B. | y=-($\frac{1}{2}$)x | C. | y=xlog2x | D. | y=x${\;}^{\frac{1}{3}}$ |
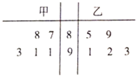 某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示:
某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示: 在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.
在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.