题目内容
4.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{4}=1({a>0})$与双曲线$\frac{x^2}{9}-\frac{y^2}{3}$=1有相同的焦点,则a的值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 4 | D. | 10 |
分析 利用椭圆、双曲线几何量之间的关系,即可求出a的值.
解答 解:由题意,a2-4=9+3,
∵a>0,
∴a=4.
故选:C.
点评 本小题考查双曲线与椭圆的关系,考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.化简:$cos(\frac{5π}{2}-α)$=( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
12.函数f(x)=$\frac{\sqrt{x}}{x-1}$的定义域是( )
| A. | [0,+∞) | B. | [0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
9.如图是一个空间几何体的三视图,则该几何体的全面积为( )
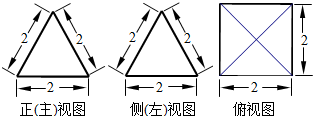

| A. | 12 | B. | 16 | C. | $\frac{{4\sqrt{3}}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
13.如果cosα=$\frac{4}{5}$,那么$sin(α+\frac{π}{4})-\frac{{\sqrt{2}}}{2}$cosα等于( )
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | ±$\frac{{2\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{10}$ | D. | ±$\frac{{3\sqrt{2}}}{10}$ |
5.数列{an}满足a1=a2=1,an+2=an+1+an恒成立,则a6=( )
| A. | 8 | B. | 13 | C. | 21 | D. | 5 |