题目内容
已知函数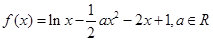 .
.
(1)若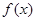 在
在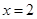 处的切线与直线
处的切线与直线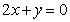 垂直,求
垂直,求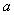 的值;
的值;
(2)若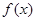 存在单调递减区间,求
存在单调递减区间,求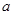 的取值范围.
的取值范围.
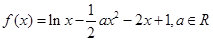 .
.(1)若
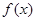 在
在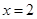 处的切线与直线
处的切线与直线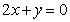 垂直,求
垂直,求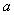 的值;
的值;(2)若
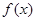 存在单调递减区间,求
存在单调递减区间,求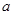 的取值范围.
的取值范围.(1)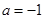 ;(2)
;(2)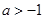 .
.
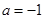 ;(2)
;(2)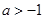 .
.试题分析:(1)先求出
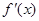 ,进而得到
,进而得到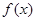 在
在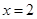 处的切线的斜率
处的切线的斜率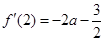 ,由两直线垂直的斜率关系式得到
,由两直线垂直的斜率关系式得到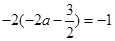 ,进而可求出
,进而可求出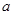 的值;(2)先将
的值;(2)先将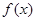 存在单调递减区间等价于
存在单调递减区间等价于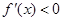 在
在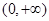 有解即也就是
有解即也就是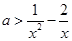 在
在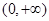 有解,也就是
有解,也就是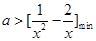 ,进而只须用二次函数的知识求出函数
,进而只须用二次函数的知识求出函数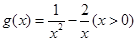 的最小值即可得出
的最小值即可得出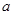 的取值范围.
的取值范围.试题解析:(1)因为
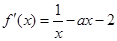
所以
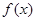 在
在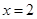 处的切线的斜率为
处的切线的斜率为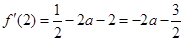
又因为
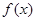 在
在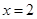 处的切线与直线
处的切线与直线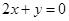 垂直,而直线
垂直,而直线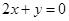 的斜率为
的斜率为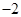
所以
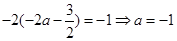
(2)
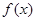 存在单调递减区间,等价于
存在单调递减区间,等价于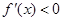 在
在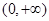 有解,即
有解,即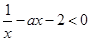 也就是
也就是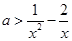 在
在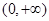 有解
有解令
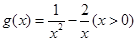 ,则只需要求
,则只需要求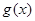 在
在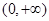 上的最小值即可即
上的最小值即可即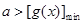
又设
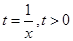 ,则
,则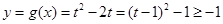 (当且仅当
(当且仅当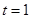 即
即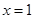 时取到等号)
时取到等号)所以

练习册系列答案
相关题目
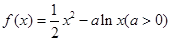 .
.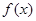 在
在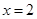 处的切线与直线
处的切线与直线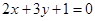 垂直,求
垂直,求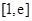 上的最大值.
上的最大值.
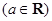 .
.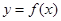 在点
在点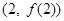 处的切线方程是y=x+ln2时,求a的值.
处的切线方程是y=x+ln2时,求a的值.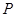 为曲线
为曲线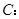
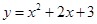 上的点,且曲线
上的点,且曲线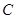 在点
在点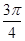 ,
,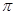 ),则点
),则点



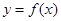 是可导函数,直线
是可导函数,直线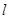 是曲线
是曲线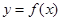 在
在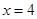 处的切线,令
处的切线,令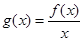 ,则
,则 .
.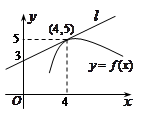
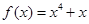 图像上一点,在A处的切线平行于直线
图像上一点,在A处的切线平行于直线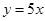 ,则A点坐标为 ;
,则A点坐标为 ;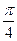 的点是( )
的点是( )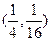
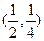
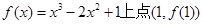 处的切线方程为 。
处的切线方程为 。