题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 经过椭圆
经过椭圆![]() 的左顶点
的左顶点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() (
(![]() )交椭圆
)交椭圆![]() 于
于![]() 两点(
两点(![]() 不同于点
不同于点![]() ).过原点
).过原点![]() 的一条直线与直线
的一条直线与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 分别交于点
分别交于点![]() .
.
(ⅰ)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(ⅱ)若![]() ,求证:点
,求证:点![]() 在一条定直线上.
在一条定直线上.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)证明见解析.
;(ⅱ)证明见解析.
【解析】
(1)将点![]() 代入直线方程可求得
代入直线方程可求得![]() ,结合离心率和椭圆
,结合离心率和椭圆![]() 关系可求得
关系可求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,
,![]()
(i)将直线![]() 与椭圆方程联立可得韦达定理的形式,利用弦长公式表示出
与椭圆方程联立可得韦达定理的形式,利用弦长公式表示出![]() ,由二次函数最大值可求得
,由二次函数最大值可求得![]() 的最大值;
的最大值;
(ii)设直线![]() ,直线
,直线![]() ,两式联立可求得
,两式联立可求得![]() ,同理可得
,同理可得![]() ,根据
,根据![]() 得到
得到![]() ,整理得
,整理得![]() ,将直线
,将直线![]() 与椭圆方程联立可得韦达定理的形式,代入上式得
与椭圆方程联立可得韦达定理的形式,代入上式得![]() ,从而得到
,从而得到![]() ,将直线
,将直线![]() 与直线
与直线![]() 联立可求得
联立可求得![]() ,进而得到结果.
,进而得到结果.
(1)设![]()
![]() 点
点![]() 在直线
在直线![]() 上
上 ![]() ,解得:
,解得:![]()
![]()
![]()
![]() 离心率
离心率![]()
![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)设![]() ,
,![]()
(i)![]()
![]() 由
由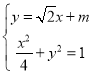 消去
消去![]() 可得:
可得:![]()
即![]() ,由
,由![]() 得:
得:![]()
![]() ,
,![]()
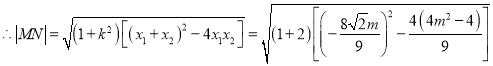
![]()
![]()
![]()
当且仅当![]() 时,
时,![]() 取到最大值
取到最大值![]()
(ii)若![]() ,则
,则![]() 为
为![]() 的中点
的中点 ![]()
设直线![]() ,直线
,直线![]()
两个方程联立可得:![]() ,解得:
,解得:![]()
同理可得:![]()
![]()
即![]()
![]()
化简得:![]() …①
…①
由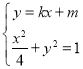 得:
得:![]() ,即
,即![]()
由![]() 得:
得:![]()
![]() ,
,![]()
代入①得:![]()
![]() ,即
,即![]()
若![]() ,则直线
,则直线![]() 过点
过点![]() ,与已知不符合
,与已知不符合
又![]()
![]()
又由![]() ,联立
,联立![]() 消去
消去![]() 得:
得:![]()
![]() 点
点![]() 在定直线
在定直线![]() 上
上

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知国家某![]() 级大型景区对拥挤等级与每日游客数量
级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]() 时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
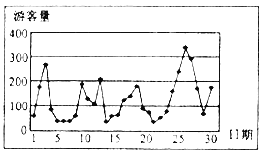
(1)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量(单位:百人) |
|
|
|
|
天数 |
| 10 | 4 | 1 |
频率 |
|
|
|
|
(2)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的频率.