Question

【题目】在四棱锥中，，，和都是边长为2的等边三角形，设在底面的射影为.

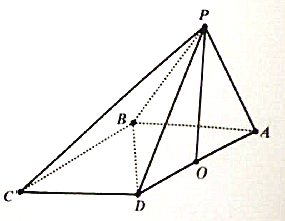
（1）求证：是中点；

（2）证明：；

（3）求点到面的距离.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）.

【解析】试题分析:（1）根据等边三角形有，依题意有平面，故，由此可知为中点.（2）由平面可得，而，即，故平面，故.（3）利用等体积法,利用（2）的结论，可求得两个面积的表达式，进而求得点到面的距离.

试题解析：（1）证明：∵和都是等边三角形，

∴，

又∵底面，

∴，

则点为的外心，又因为是直角三角形，

∴点为中点.

（2）证明：由（1）知，点在底面的射影为点，点为中点，

于是面，

∴，

∵在中，，，

∴，

又，∴，

从而即，

由，得面，

∴.

（3）∵，

∴是平行四边形，

在中，∵，∴，

由（2）知：面，，

由，，

∴，

∴，

.

设点到面的距离为，由等体积法，

∴，

∴.

即点到面的距离为1.