题目内容
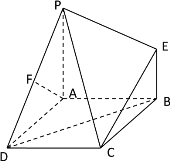
【题目】如图,四棱锥![]() 的底面是边长为2的菱形,
的底面是边长为2的菱形,![]() 底面
底面![]() .
.
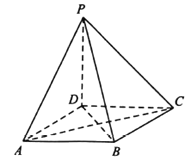
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)通过AC⊥BD与PD⊥AC可得![]() 平面
平面![]() ;
;
(2)由题先得出∠PBD是直线PB与平面ABCD所成的角,即∠PBD=45°,则可先求出菱形ABCD的面积,进而可得四棱锥P- ABCD的体积.
解:(1)因为四边形ABCD是菱形,所以AC⊥BD,
又因为PD⊥平面ABCD,![]() 平面ABCD,
平面ABCD,
所以PD⊥AC,又![]() ,
,
故AC⊥平面PBD;
(2)因为PD⊥平面ABCD,
所以∠PBD是直线PB与平面ABCD所成的角,
于是∠PBD=45°,
因此BD=PD=2.又AB= AD=2,
所以菱形ABCD的面积为![]() ,
,
故四棱锥P- ABCD的体积![]() .
.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目