题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,
点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,![]() ,
,![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BDE;
平面BDE;
![]() Ⅱ
Ⅱ![]() 求直线MN到平面BDE的距离;
求直线MN到平面BDE的距离;
![]() Ⅲ
Ⅲ![]() 求二面角
求二面角![]() 的大小.
的大小.
【答案】![]() Ⅰ
Ⅰ![]() 见解析;
见解析;![]() Ⅱ
Ⅱ![]() ;
;![]() Ⅲ
Ⅲ![]()
【解析】
![]() Ⅰ
Ⅰ![]() 以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明
以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明![]() 平面BDE.
平面BDE.
![]() Ⅱ
Ⅱ![]() 求出
求出![]() 0,
0,![]() ,利用向量法得直线MN到平面BDE的距离
,利用向量法得直线MN到平面BDE的距离![]() .
.
![]() Ⅲ
Ⅲ![]() 求出平面BDE的法向量和平面DEP的法向量,利用向量法能求出二面角
求出平面BDE的法向量和平面DEP的法向量,利用向量法能求出二面角![]() 的大小.
的大小.
![]() Ⅰ
Ⅰ![]() 在三棱锥
在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 点D,E分别为棱PA,PC的中点,
点D,E分别为棱PA,PC的中点,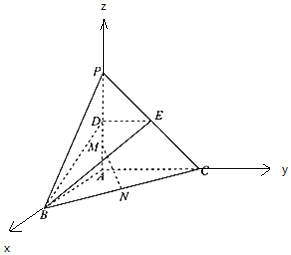
M是线段AD的中点,N是线段BC的中点,![]() ,
,
![]() .
.
以A为原点,AB为x轴,AC为y轴,AP为z轴,
建立空间直角坐标系,
![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 4,
4,![]() ,
,
![]() 2,
2,![]() ,
,![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,
![]() 2,
2,![]() ,
,
![]() 2,
2,![]() ,
,![]() 0,
0,![]() ,
,
![]() 2,
2,![]() ,
,
设平面BDE的法向量![]() y,
y,![]() ,
,
则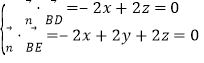 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
![]() ,
,![]() 平面BDE,
平面BDE,
![]() 平面BDE.
平面BDE.
![]() Ⅱ
Ⅱ![]() ,0,
,0,![]() ,
,
![]() 直线MN到平面BDE的距离:
直线MN到平面BDE的距离:
![]() .
.
![]() Ⅲ
Ⅲ![]() 平面BDE的法向量
平面BDE的法向量![]() 0,
0,![]() ,
,
平面DEP的法向量![]() 0,
0,![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,
,
则![]() .
.
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目



