题目内容
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据椭圆几何意义得![]() ,再根据离心率为
,再根据离心率为![]() 得
得![]() (2)设直线
(2)设直线![]() 点斜式方程,与椭圆方程联立方程组,结合韦达定理以及弦长公式求底边AB长,再根据点到直线距离公式得高,最后根据三角形面积公式列方程,解出直线斜率,注意验证斜率不存在时是否满足题意
点斜式方程,与椭圆方程联立方程组,结合韦达定理以及弦长公式求底边AB长,再根据点到直线距离公式得高,最后根据三角形面积公式列方程,解出直线斜率,注意验证斜率不存在时是否满足题意
试题解析:解:(Ⅰ)设椭圆![]() 的方程为:
的方程为: ![]()
![]() ,
,
由已知:  得:
得: ![]() ,
, ![]() ,
,
所以,椭圆![]() 的方程为:
的方程为: ![]() .
.
(Ⅱ)由已知直线![]() 过左焦点
过左焦点![]() .
.
当直线![]() 与
与![]() 轴垂直时,
轴垂直时,  ,
,  ,此时
,此时![]() ,
,
则![]() ,不满足条件.
,不满足条件.
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为:
的方程为: ![]()
由 得
得![]()
所以![]() ,
, ![]() ,
,
而![]() ,
,
由已知![]() 得
得![]() ,
,
![]() ,
,
所以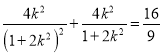 ,则
,则![]() ,所以
,所以![]() ,
,
所以直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
预计在今后的销售中,销量与单价仍然服从这种线性相关关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为( )
(附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为 .参考数值:
.参考数值:![]() ,
,![]() )
)
A. 9.4元 B. 9.5元 C. 9.6元 D. 9.7元