Question

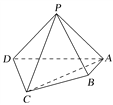
【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD＝60°，AB＝PA＝2，PA⊥平面ABCD，E是PC的中点，F是AB的中点．

（1）求证：BE∥平面PDF；

（2）求证：平面PDF⊥平面PAB；

（3）求BE与平面PAC所成的角．

Answer 1

【答案】（1）证明见解析（2）证明见解析（3）45°．

【解析】

（1）取PD的中点为M，连接ME，MF，证明BE∥MF，BE∥平面PDF即得证；

（2）先证明DF⊥平面PAB，平面PDF⊥平面PAB即得证；

（3）利用定义法求BE与平面PAC所成的角．

（1）证明：取PD的中点为M，连接ME，MF，

∵E是PC的中点，∴ME是△PCD的中位线．

∴ME∥CD，MECD．

又∵F是AB的中点，且由于ABCD是菱形，

∴AB∥CD，AB＝CD，∴ME∥FB，且ME＝FB．

∴四边形MEBF是平行四边形，∴BE∥MF．

∵BE平面PDF，MF平面PDF，

∴BE∥平面PDF．

（2）证明：∵PA⊥平面ABCD，DF平面ABCD，

∴DF⊥PA．连接BD，

∵底面ABCD是菱形，∠BAD＝60°，∴△DAB为正三角形．

∵F是AB的中点，∴DF⊥AB．

∵PA∩AB＝A，∴DF⊥平面PAB．

∵DF平面PDF，∴平面PDF⊥平面PAB．

（3）连结BD交AC于O，∵底面ABCD是菱形，∴AC⊥BD，

∵PA⊥平面ABCD，∴PA⊥BD，∴BD⊥平面PAC．

∴OB⊥OE，即OE是BE在平面PAC上的射影．

∴∠BEO是BE与平面PAC所成的角．

∵O，E，分别是中点，∴OEAP＝1，OD1，

∴Rt△BOE为等腰直角三角形，∴∠BEO＝45°，

即BE与平面PAC所成的角的大小为45°．