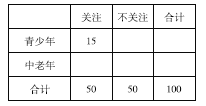
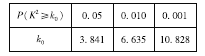
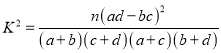题目内容
【题目】如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 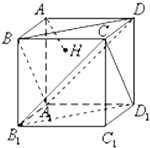
A.点H是△A1BD的垂心
B.AH的延长线经过点C1
C.AH垂直平面CB1D1
D.直线AH和BB1所成角为45°
【答案】D
【解析】解:对于A,因为三棱锥A﹣A1BD是正三棱锥,故顶点A在底面的射影是底面正三角形的中心,所以点H是也是△A1BD的垂心,故A正确;
对于B,因为三棱锥C1﹣A1BD是正三棱锥,而H是底面的中心,故C1H是正三棱锥C1﹣A1BD的高线,因为经过点H与平面A1BD垂直的直线有且只有一条,故A、H、C1三点共线,即AH的延长线经过点C1 , 故B正确;
对于C,因为平面A1BD∥平面CB1D1 , 而AH垂直平面A1BD,所以根据面面平行的性质,可得AH垂直平面CB1D1 , 故C正确;
对于D,可在正三棱锥A﹣A1BD中,算出cos∠A1AH= ![]() ,结合AA1∥BB1 , 可得直线AH和BB1所成角为arccos
,结合AA1∥BB1 , 可得直线AH和BB1所成角为arccos ![]() ,故D不正确.
,故D不正确.
故选D
因为三棱锥A﹣A1BD是正三棱锥,所以H是正三角形﹣A1BD的中心,故A正确;根据正三棱锥A﹣A1BD和正三棱锥C1﹣A1BD的高线都经过H点,结合垂线的唯一性可得B正确;根据平面A1BD∥平面CB1D1 , 结合面面平行的性质,得到C正确;通过计算可得直线AH和BB1所成角为arccos ![]() ,故D不正确.
,故D不正确.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目