题目内容
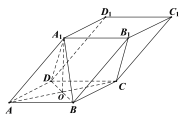
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
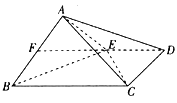
(Ⅰ)证明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;
(II)![]()
【解析】
(Ⅰ)取BC的中点G,连接FG,EG,证明四边形EGCD为平行四边形,得EG∥平面ACD,再证明FG∥平面ACD,可得平面EFG∥平面ACD,从而得到EF∥平面ACD;
(Ⅱ)求解三角形证明BA⊥AE,取BE的中点H,连接AH,HC,证明AH⊥平面BCDE.以H为坐标原点,以过点H且平行于CD的直线为x轴,以过点H且平行于BC的直线为y轴,HA所在直线为z轴建立空间直角坐标系,求出平面ACD的一个法向量,再求出直线BC的方向向量,由两向量所成角的余弦值可得直线BC与平面ACD所成角的正弦值.
解:证明:(I)作![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
故![]() ,则
,则![]() 平面
平面![]() ,
,
又![]()
![]() 为
为![]() 的中点,
的中点,![]() ,则
,则![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
(II)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,则
,则![]() ,
,
作![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,
,![]() 平面
平面![]() .
.
以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,以过点
轴,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
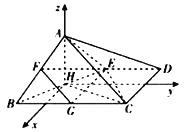
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则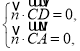 即
即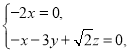
可得![]() ,
,
直线![]() 的方向向量
的方向向量![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则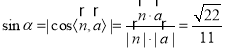 ,
,
综上,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: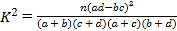 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |