题目内容
【题目】为了解高中学生对数学课是否喜爱是否和性别有关，随机调查220名高中学生，将他们的意见进行了统计，得到如下的
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
（1）根据上面的列联表判断，能否有
的把握认为“喜爱数学课与性别”有关；
（2）为培养学习兴趣，从不喜爱数学课的学生中进行进一步了解，从上述调查的不喜爱数学课的人员中按分层抽样抽取6人，再从这6人中随机抽出2名进行电话回访，求抽到的2人中至少有1名“男生”的概率.
参考公式：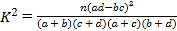
.
P（ | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【答案】（1）有（2）
【解析】
（1）由列联表数据，根据参考公式求出
观测值，结合提供数据，即可得出结论；
（2）分层抽样男生应抽取2人，女生应抽取4人，按男女生编号，列出从6人中任取2人的所有情况，确定至少有1名男生的抽取方法个数，由古典概型的概率公式，即可求解.
（1）根据列联表数据，
计算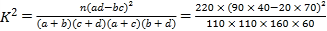
，
所以有
的把握认为“喜爱数学课与性别有关”.
（2）从不喜爱数学课的人员中按分层抽样法抽取6人，
男生应抽取2人，设为A，B，女生应抽取4人，设为a，b，c，d，
从中随机抽出2人，总的情况为
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15种，
至少有1名男生的情况数为9，
所以根据古典概型的公式，得
.
练习册系列答案
教材全解字词句篇系列答案
相关题目
