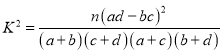题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若方程![]() 没有实数解,求实数
没有实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() 在
在![]() 单调递减,
单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
(II)![]()
【解析】
(I)先对函数求导,结合导数与单调性的关系即可求解函数的单调性;
(II)由![]() 没有实数解,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况,即可求解.
没有实数解,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况,即可求解.
(Ⅰ)当![]() 时,
时,![]() ,函数的定义域为
,函数的定义域为![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,
,
又因为函数![]() 单调递增,
单调递增,
所以在![]() 上,
上,![]() ,
,![]() 单调递减;
单调递减;
在![]() 上,
上,![]() ,
,![]() 单调递增.
单调递增.
(II)方程![]() 没有实数解,
没有实数解,
即方程![]() 没有实数解,
没有实数解,
设函数![]() ,
,
![]() ,
,
(i)当![]() 时,
时,![]() ,函数
,函数![]() 没有零点;
没有零点;
(ii)当![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() ,且
,且![]() ,函数
,函数![]() 有零点;
有零点;
(iii)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,
令![]() ,得
,得![]() ,
,
即函数![]() 没有零点,
没有零点,
综上所述,若函数![]() 没有零点,
没有零点,
即方程![]() 没有实数解,
没有实数解,
故实数![]() 的取值范围为
的取值范围为![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】2019年第一期中国青年阅读指数数据显示,从阅读需求的角度,排名前三的阅读领域分别为文学、哲学及社会科学和历史.某学校从文科生和理科生中选取了经常阅读的学生进行了假期阅读内容和阅读时间方面的调查,得到以下数据.
学生所学文理与阅读内容列联表
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 70 | 130 | 200 |
文科生 | 45 | 55 | 100 |
合计 | 115 | 185 | 300 |
(Ⅰ)判断能否有![]() 把握认为学生所学文理与阅读内容有关?
把握认为学生所学文理与阅读内容有关?
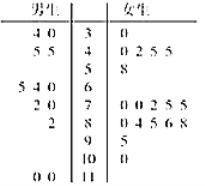
(Ⅱ)从阅读时间大于30分钟的被调查同学中随机选取30名学生,其阅读时间(分钟)整理成如图所示的茎叶图,并绘制日均阅读时间分布表;
其中30名同学的日均阅读时间分布表(单位:分钟)
阅读时间 |
|
|
|
男生人数 | 4 |
| 2 |
女生人数 |
| 10 | 2 |
求出![]() ,
,![]() 的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
(Ⅲ)从(Ⅱ)中日均阅读时间高于90分钟的同学中随机选取2人介绍阅读体会,求这2人性别相同的概率.
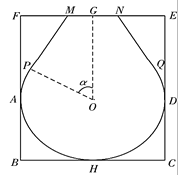
参考公式: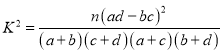 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)调查组从该样本的城镇居民中按分层抽样抽取出7人,参加一次阅读交流活动,若活动主办方从这7位居民中随机选取2人作交流发言,求被选中的2位居民都是经常阅读居民的概率.
附: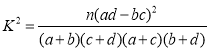 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |