题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 轴为曲线
轴为曲线![]() 的切线;
的切线;
(2)用![]() 表示
表示![]() 、
、![]() 中的最大值,设函数
中的最大值,设函数![]() ,当
,当![]() 时,讨论
时,讨论![]() 零点的个数.
零点的个数.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)设切点坐标为![]() ,然后根据
,然后根据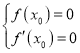 可解得实数
可解得实数![]() 的值;
的值;
(2)令![]() ,
,![]() ,然后对实数
,然后对实数![]() 进行分类讨论,结合
进行分类讨论,结合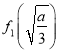 和
和![]() 的符号来确定函数
的符号来确定函数![]() 的零点个数.
的零点个数.
(1)![]() ,
,![]() ,
,
设曲线![]() 与
与![]() 轴相切于点
轴相切于点![]() ,则
,则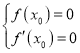 ,
,
即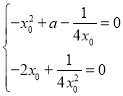 ,解得
,解得 .
.
所以,当![]() 时,
时,![]() 轴为曲线
轴为曲线![]() 的切线;
的切线;
(2)令![]() ,
,![]() ,
,
则![]() ,
,![]() ,由
,由![]() ,得
,得![]() .
.
当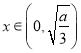 时,
时,![]() ,此时,函数
,此时,函数![]() 为增函数;当
为增函数;当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 为减函数.
为减函数.
![]() ,
,![]() .
.
①当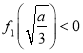 ,即当
,即当![]() 时,函数
时,函数![]() 有一个零点;
有一个零点;
②当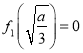 ,即当
,即当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
③当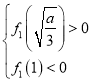 ,即当
,即当![]() 时,函数
时,函数![]() 有三个零点;
有三个零点;
④当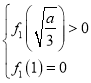 ,即当
,即当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
⑤当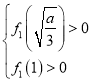 ,即当
,即当![]() 时,函数
时,函数![]() 只有一个零点.
只有一个零点.
综上所述,当![]() 或
或![]() 时,函数
时,函数![]() 只有一个零点;
只有一个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 时,函数
时,函数![]() 有三个零点.
有三个零点.

练习册系列答案
相关题目