题目内容
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点
)的焦点![]() 到点
到点![]() 的距离为
的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
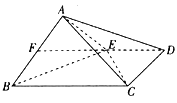
(2)过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在第一和第二象限内,求
分别在第一和第二象限内,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)因为![]() ,可得
,可得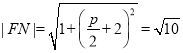 ,即可求得答案;
,即可求得答案;
(2)分别设![]() 、
、![]() 的斜率为
的斜率为![]() 和
和![]() ,切点
,切点![]() ,
,![]() ,可得过点
,可得过点![]() 的抛物线的切线方程为
的抛物线的切线方程为![]() :
:![]() ,联立直线
,联立直线![]() 方程和抛物线
方程和抛物线![]() 方程,得到关于
方程,得到关于![]() 一元二次方程,根据
一元二次方程,根据![]() ,求得
,求得![]() ,
,![]() ,进而求得切点
,进而求得切点![]() ,
,![]() 坐标,根据两点间距离公式求得
坐标,根据两点间距离公式求得![]() ,根据点到直线距离公式求得点
,根据点到直线距离公式求得点![]() 到切线
到切线![]() 的距离
的距离![]() ,进而求得
,进而求得![]() 的面积.
的面积.
(1)![]()
![]() ,
,
![]()
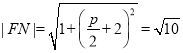 ,
,
![]() 解得
解得![]() ,
,
![]() 抛物线
抛物线![]() 的方程为
的方程为![]() .
.
(2)由题意可知,![]() 、
、![]() 的斜率都存在,分别设为
的斜率都存在,分别设为![]() 和
和![]() ,切点
,切点![]() ,
,
![]() ,
,
![]() 过点
过点![]() 的抛物线的切线
的抛物线的切线![]() :
:![]() ,
,
![]() 由
由![]() ,消掉
,消掉![]() ,
,
可得![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() 解得
解得![]() ,
,![]() ,
,
又![]() 由
由![]() ,
,
得![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() 同理可得
同理可得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 切线
切线![]() 的方程为
的方程为![]() ,
,
![]() 点
点![]() 到切线
到切线![]() 的距离为
的距离为![]() ,
,
![]()
![]() ,
,
即![]() 的面积为
的面积为![]() .
.

【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间
岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”
内的人分别称为“青少年人”和“中老年人”![]() 经统计“青少年人”和“中老年人”的人数之比为
经统计“青少年人”和“中老年人”的人数之比为![]() ,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.
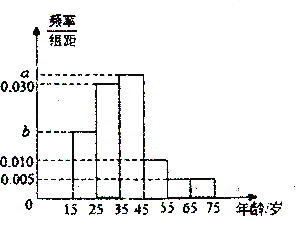
(1)求图中a,b的值;
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
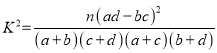
P(K2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |