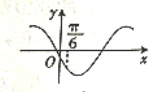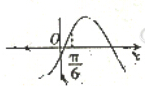题目内容
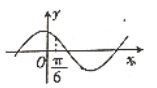
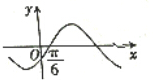
7．
已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，且当x＜0时，函数的部分图象如图所示，则不等式xf（x）＜0的解集是（ ）| A． | {x|-2＜x＜-1，或1＜x＜2} | B． | {x|-2＜x＜-1，或0＜x＜1，或x＞2} | ||
| C． | {x|x＜-2，或1＜x＜2} | D． | {x|x＜-2，或-1＜x＜0，或0＜x＜1，或x＞2} |
分析 设g（x）=xf（x），判断函数的奇偶性，利用函数奇偶性的对称性求出当x＜0时的解集即可得到结论．
解答 解：设g（x）=xf（x），
∵函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，
∴g（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，
则当x＜0时，xf（x）＜0等价为f（x）＞0，此时x＜-2或-1＜x＜0，
∵g（x）是偶函数，
∴g（x）＜0得解为x＜-2，或-1＜x＜0，或0＜x＜1，或x＞2，
即不等式xf（x）＜0的解集是{x|x＜-2，或-1＜x＜0，或0＜x＜1，或x＞2}，
故选：D．
点评 本题主要考查不等式的求解，根据函数奇偶性的性质是解决本题的关键．
练习册系列答案
学习实践园地系列答案
相关题目
