题目内容
12.已知函数f(x)=$\frac{{a}^{x}-{a}^{-x}}{2}$,g(x)=$\frac{{a}^{x}+{a}^{-x}}{2}$,(其中a>0,且 a≠1).(1)求证f2(x)+g2(x)=g(2x);
(2)判断函数f(x)和g(x)的奇偶性.
分析 (1)根据指数幂的运算法则进行化简即可证明.
(2)根据函数奇偶性的定义进行判断即可.
解答 解:(1)f2(x)+g2(x)=($\frac{{a}^{x}-{a}^{-x}}{2}$)2+($\frac{{a}^{x}+{a}^{-x}}{2}$)2=$\frac{{a}^{2x}-2+{a}^{-2x}}{4}$+$\frac{{a}^{2x}+2+{a}^{-2x}}{4}$=$\frac{{a}^{2x}+{a}^{-2x}}{2}$=g(2x).
(2)f(-x)=$\frac{{a}^{-x}-{a}^{x}}{2}$=-$\frac{{a}^{x}-{a}^{-x}}{2}$=-f(x),则f(x)为奇函数,
g(-x)=$\frac{{a}^{x}+{a}^{-x}}{2}$=g(x),则g(x)为偶函数.
点评 本题主要考查函数奇偶性的判断以及等式的证明,比较基础.

练习册系列答案
相关题目
2.若无论x取何值时,不等式x2+kx+4>0都成立,则k的取值范围为( )
| A. | (-4,4) | B. | (-4,0) | C. | (0,4) | D. | (-2,2) |
3.某高三学生在连续五次月考中,其数学成绩统计如下:
90 90 93 94 93
则该学生这五次月考数学成绩平均值和方差分别为( )
90 90 93 94 93
则该学生这五次月考数学成绩平均值和方差分别为( )
| A. | 92,2.8 | B. | 92,2 | C. | 93,2 | D. | 93,2.8 |
7.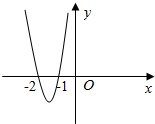 已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
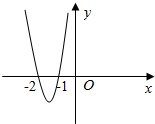 已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )| A. | {x|-2<x<-1,或1<x<2} | B. | {x|-2<x<-1,或0<x<1,或x>2} | ||
| C. | {x|x<-2,或1<x<2} | D. | {x|x<-2,或-1<x<0,或0<x<1,或x>2} |
4.在等差数列{an}中,已知a3=9,d=3,an=30,则n等于( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |