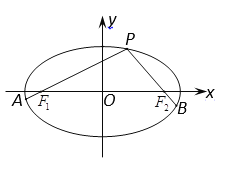
题目内容
【题目】已知点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(2)动直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点,证明
为坐标原点,证明![]() 为定值.
为定值.
【答案】(1)![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1)设![]() ,根据点
,根据点![]() 在线段
在线段![]() 上,且
上,且![]() ,得到
,得到![]() ,
,![]() 的坐标,再由
的坐标,再由![]() 建立x,y方程即可所求.
建立x,y方程即可所求.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,根据
轴对称,根据![]() 在椭圆上和
在椭圆上和![]() ,求得坐标即可,当直线
,求得坐标即可,当直线![]() 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为![]() ,将
,将![]() 代入方程
代入方程![]() 中,利用弦长公式求得
中,利用弦长公式求得![]() ,点
,点![]() 到直线
到直线![]() 的距离,由
的距离,由![]() 得到k,m的关系,再利用韦达定理求解即可.
得到k,m的关系,再利用韦达定理求解即可.
(1)设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,
轴对称,
所以![]() ,
,![]() .
.
因为![]() ,在椭圆上,所以有
,在椭圆上,所以有![]() ,
,
又因为![]() ,
,
所以![]() ,
,
解得![]() ,
,![]() ,
,
此时![]() ,
,![]() ,
,
![]()
②当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,由题意
,由题意![]() .
.
将![]() 代入方程
代入方程![]() 中,
中,
整理得![]() ,
,
![]() ①
①
![]() ,
,![]() ,
,
则![]() .
.
因为点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
得![]() 且符合①式,
且符合①式,
此时![]() ,
,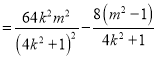
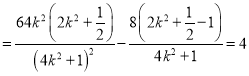 ,
,
![]() ,
,
所以![]() ,
,
综上所述,![]() (定值)
(定值)

练习册系列答案
相关题目