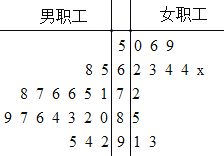
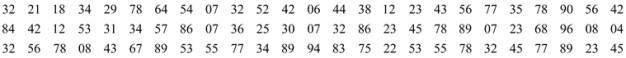题目内容
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
【答案】![]()
![]() (或2)
(或2)
【解析】
由已知得△PAC为正三角形,取PC的中点G,得AG⊥PC,且AG![]() .然后证明AG⊥EF,且求得AG与EF的长度,可得截面四边形的面积;再求出四棱锥P﹣AEGF的体积与原正四棱锥的体积,则平面α将此正四棱锥分成的两部分体积的比值可求.
.然后证明AG⊥EF,且求得AG与EF的长度,可得截面四边形的面积;再求出四棱锥P﹣AEGF的体积与原正四棱锥的体积,则平面α将此正四棱锥分成的两部分体积的比值可求.
解:如图,
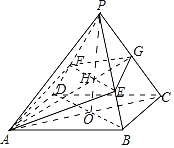
在正四棱锥P﹣ABCD中,由底面边长为2,侧棱长为![]() ,
,
可得△PAC为正三角形,取PC的中点G,得AG⊥PC,且AG![]() .
.
设过AG与PC垂直的平面交PB于E,交PD于F,连接EF,
则EG⊥PC,FG⊥PC,可得Rt△PGE≌Rt△PGF,得GE=GF,PE=PF,
在△PAE与△PAF中,由PA=PA,PE=PF,∠APE=∠APF,得AE=AF.
∴AG⊥EF.
在等腰三角形PBC中,由PB=PC=2![]() ,BC=2,得cos∠BPC
,BC=2,得cos∠BPC![]() ,
,
则在Rt△PGE中,得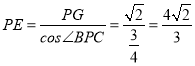 .
.
同理PF![]() ,则EF∥DB,得到
,则EF∥DB,得到![]() .
.
∴![]() ;
;
则![]() .
.
又![]() ,
,
∴平面α将此正四棱锥分成的上下两部分体积的比为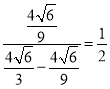 .
.
故答案为:![]() ;
;![]() (或2).
(或2).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目