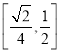Question

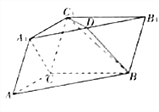
【题目】如图，在三棱柱ABC﹣A1B1C1中，已知四边形AA1C1C为矩形，AA1＝6，AB＝AC＝4，∠BAC＝∠BAA1＝60°，∠A1AC的角平分线AD交CC1于D.

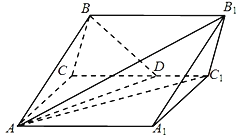
（1）求证：平面BAD⊥平面AA1C1C；

（2）求二面角A﹣B1C1﹣A1的余弦值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）过点D作DE∥AC交AA1于E，连接CE，BE，设AD∩CE＝O，连接BO，推导出DE⊥AE，四边形AEDC为正方形，CE⊥AD，推导出△BAC≌△BAE，从而BC＝BE，CE⊥BO，从而CE⊥平面BAD，由此能证明平面BAD⊥平面AA1C1C.

（2）推导出BO⊥AD，BO⊥CE，从而BO⊥平面AA1C1C，建立空间直角坐标系O﹣xyz，利用向量法能求出二面角A﹣B1C1﹣A1的余弦值.

解：（1）如图，过点D作DE∥AC交AA1于E，连接CE，BE，

设AD∩CE＝O，连接BO，∵AC⊥AA1，∴DE⊥AE，

又AD为∠A1AC的角平分线，∴四边形AEDC为正方形，∴CE⊥AD，

又∵AC＝AE，∠BAC＝∠BAE，BA＝BA，∴BAC≌BAE，∴BC＝BE，

又∵O为CE的中点，∴CE⊥BO，

又∵AD，BO平面BAD，AD∩BO＝O，∴CE⊥平面BAD.

又∵CE平面AA1C1C，∴平面BAD⊥平面AA1C1C.

（2）在ABC中，∵AB＝AC＝4，∠BAC＝60°，∴BC＝4，

在RtBOC中，∵，∴，

又AB＝4，，∵BO2+AO2＝AB2，∴BO⊥AD，

又BO⊥CE，AD∩CE＝O，AD，CE平面AA1C1C，∴BO⊥平面AA1C1C，

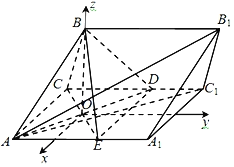
故建立如图空间直角坐标系O﹣xyz，

则A（2，﹣2，0），A1（2，4，0），C1（﹣2，4，0），，

∴，，，

设平面AB1C1的一个法向量为，

则，∴，

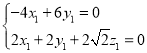令x1＝6，得，

设平面A1B1C1的一个法向量为，

则，∴，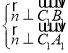

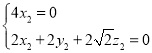令，得，

∴，

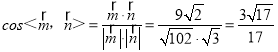故二面角A﹣B1C1﹣A1的余弦值为.