Question

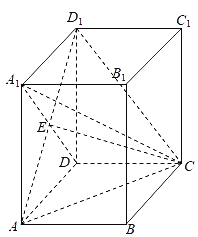
【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是矩形，A1D与AD1交于点E，AA1＝AD＝2AB＝4.

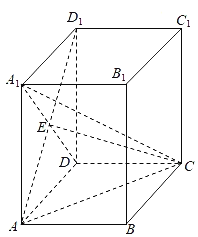
（1）证明：AE⊥平面ECD.

（2）求点C1到平面AEC的距离.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）证明CD⊥平面ADD1A1可得CD⊥AE，根据AA1＝AD可得AE⊥DE，

故而AE⊥平面EDC；

（2）根据V列方程计算C1到平面AEC的距离.

（1）证明：∵四边形ABCD是矩形，∴CD⊥AD，

∵AA1⊥平面ABCD，CD平面ABCD，

∴AA1⊥CD，又AA1∩AD＝A，

∴CD⊥平面ADD1A1，

∴CD⊥AE，

∵四边形ADD1A1是平行四边形，∴E是A1D的中点，

∵AA1＝AD，∴AE⊥DE，

又CD∩DE＝D，

∴AE⊥平面ECD.

（2）连接CD1，则点C1到平面AEC的距离即为点C1到平面ACD1的距离.

在△ACD1中，AC＝2，AD1＝4，CD1＝2，

∴CE⊥AD1，且CE2，

∴S4，

设C1到平面ACD1的距离为h，则V.

又V，

∴4h＝16，即h.

∴点C1到平面AEC的距离为.